《2025年全品学练考九年级数学上册苏科版江苏专版》

11.(2024南京期中)如图2-4-39,$□ BCDE$的顶点B,C,D在半圆O上,顶点E在直径AB上,连接AD.若$∠CDE= 68^{\circ }$,则$∠ADE$的度数为______44$^{\circ }$.

答案： 44

12.(2023南京期末)如图2-4-40,$\triangle ABC内接于\odot O$,$\triangle ABC的外角∠ABE的平分线交\odot O$于点D,射线AD交CB的延长线于点E.若$∠BAC= 28^{\circ }$,$BC= BD$,则$∠E$的度数为______40$^{\circ }$.

答案： 40

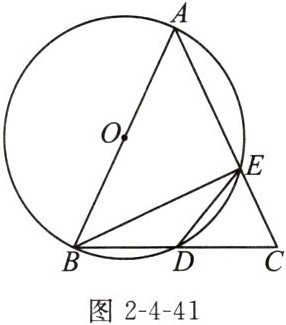
13.(2024南京期中)如图2-4-41,$\triangle ABC$中,$AB= AC$,以AB为直径的$\odot O$交BC于点D,交AC于点E.
(1)求证：$BD= CD$；
(2)若$∠BAC= 50^{\circ }$,求$∠EBC和∠EDC$的度数.

答案：

(1)证明:如图,连接AD.

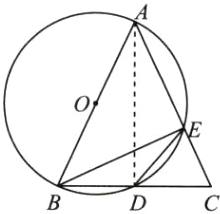
∵AB是$\odot O$的直径,
∴$\angle ADB = 90^{\circ}$,
∴$AD \perp BC$.
又
∵$AB = AC$,
∴$BD = CD$.
(2)$\angle EBC = 25^{\circ}$,$\angle EDC = 50^{\circ}$

14. 新考法探究性“求知”学习小组在学完“圆内接四边形的对角互补”这个结论后进行了如下的探究活动：
(1)如图2-4-42①,点A,B,C在$\odot O$上,点D在$\odot O$外,线段AD,CD与$\odot O$分别交于点E,F,试猜想$∠B+∠D$______$180^{\circ }$(请填“＞”“＜”或“=”).
(2)如图②,点A,B,C在$\odot O$上,点D在$\odot O$内,此时(1)中猜想的结论还成立吗？若成立,请予以证明；若不成立,请写出你的结论并予以证明.

答案：
解:
(1)$＜$
(2)结论不成立,$\angle B + \angle D ＞ 180^{\circ}$.证明如下:
如图,延长CD交$\odot O$于点G,连接AG.

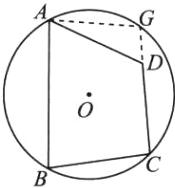
∵四边形ABCG是$\odot O$的内接四边形,
∴$\angle B + \angle G = 180^{\circ}$.
∵$\angle ADC$是$\triangle ADG$的一个外角,
∴$\angle ADC ＞ \angle G$,
∴$\angle B + \angle ADC ＞ 180^{\circ}$.