第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
(2024 泰州模拟)学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列 3 个问题时都用到了同一种数学思想方法:
问题 1:若 $ a - 2b = 3 $,求 $ 2a - 4b + 1 $ 的值.
解决思路:$ 2a - 4b + 1 = 2(a - 2b) + 1 = 2 × 3 + 1 = 7 $.
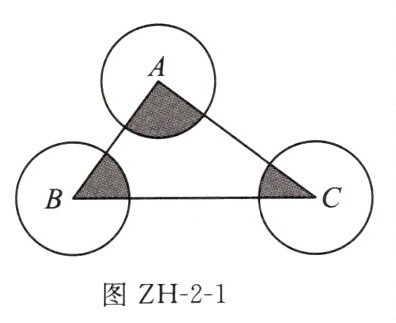
问题 2:如图 ZH - 2 - 1,分别以 $ \triangle ABC $ 的 3 个顶点为圆心,2 为半径画圆,求图中 3 块阴影面积之和.
解决思路:将 3 块阴影扇形拼成一个半径为 2 的半圆,则阴影面积为 $ 2\pi $.
问题 3:已知 $ a ^ { 2 } + b ^ { 2 } = 3ab ( a > b > 0 ) $,求 $ \frac { a ^ { 2 } - b ^ { 2 } } { a b } $ 的值.
解题思路:对已知条件进行恒等变形,$ a ^ { 2 } + b ^ { 2 } + 2ab = 5ab $,则 $ ( a + b ) ^ { 2 } = 5ab $.
因为 $ a > b > 0 $,所以 $ a + b = \sqrt { 5ab } $,类似可以得到 $ a - b =… $.
(1)方框内 3 个问题的解决都用到了
A. 分类讨论 B. 数形结合 C. 整体 D. 从特殊到一般
(2)方框内问题 3 中 $ \frac { a ^ { 2 } - b ^ { 2 } } { a b } $ 的值为
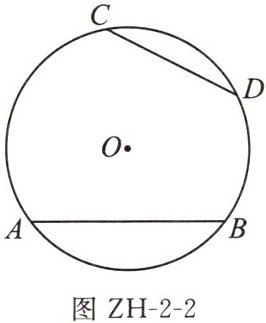
(3)如图 ZH - 2 - 2,已知 $ \odot O $ 的半径为 5, $ AB $, $ CD $ 是 $ \odot O $ 的弦,且 $ AB = 8 $, $ CD = 6 $,求 $ \overparen { A B } $ 与 $ \overparen { C D } $ 的长度之和.
小明在反思学习时,发现解决下列 3 个问题时都用到了同一种数学思想方法:
问题 1:若 $ a - 2b = 3 $,求 $ 2a - 4b + 1 $ 的值.
解决思路:$ 2a - 4b + 1 = 2(a - 2b) + 1 = 2 × 3 + 1 = 7 $.
问题 2:如图 ZH - 2 - 1,分别以 $ \triangle ABC $ 的 3 个顶点为圆心,2 为半径画圆,求图中 3 块阴影面积之和.
解决思路:将 3 块阴影扇形拼成一个半径为 2 的半圆,则阴影面积为 $ 2\pi $.
问题 3:已知 $ a ^ { 2 } + b ^ { 2 } = 3ab ( a > b > 0 ) $,求 $ \frac { a ^ { 2 } - b ^ { 2 } } { a b } $ 的值.
解题思路:对已知条件进行恒等变形,$ a ^ { 2 } + b ^ { 2 } + 2ab = 5ab $,则 $ ( a + b ) ^ { 2 } = 5ab $.
因为 $ a > b > 0 $,所以 $ a + b = \sqrt { 5ab } $,类似可以得到 $ a - b =… $.
(1)方框内 3 个问题的解决都用到了
C
的数学思想方法(从下列选项中选一个);A. 分类讨论 B. 数形结合 C. 整体 D. 从特殊到一般
(2)方框内问题 3 中 $ \frac { a ^ { 2 } - b ^ { 2 } } { a b } $ 的值为
$\sqrt{5}$
;(3)如图 ZH - 2 - 2,已知 $ \odot O $ 的半径为 5, $ AB $, $ CD $ 是 $ \odot O $ 的弦,且 $ AB = 8 $, $ CD = 6 $,求 $ \overparen { A B } $ 与 $ \overparen { C D } $ 的长度之和.
$5\pi$


答案:
(1)C
(2)$\sqrt{5}$
(3)$5\pi$
(1)C
(2)$\sqrt{5}$
(3)$5\pi$
查看更多完整答案,请扫码查看


