《2025年全品学练考九年级数学上册苏科版江苏专版》

9. 在⊙O中,若最长的弦长为16cm,则⊙O的半径是(B)
A. 4cm
B. 8cm
C. 16cm
D. 32cm

答案： B

10. (教材习题2.1 T8变式)如图2-1-14,四边形PAOB是矩形,且点A在OM上,点B在ON上,点P在以点O为圆心的$\overset{\frown}{MN}$上,且不与点M,N重合,当点P在$\overset{\frown}{MN}$上移动时,矩形PAOB的形状随之变化,则AB的长(C)

A. 逐渐变大
B. 逐渐变小
C. 不变
D. 不能确定

答案： C

11. 如图2-1-15,在△ABC中,∠ACB= 90°,∠A= 40°,以顶点C为圆心,CB的长为半径作圆交AB于点D,连接CD,则∠ACD= ______10°.

答案： 10°

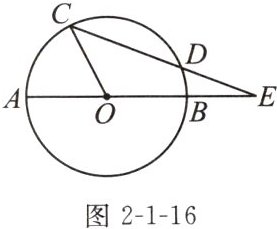
12. (2023淮安期中)如图2-1-16,⊙O的直径AB的延长线与弦CD的延长线交于点E,连接OC,若DE= OB,∠AOC= 63°,求∠E的度数.21°

答案： 21°

13. 核心素养模型观念、应用意识某公园计划建一个形状如图2-1-17①所示的喷水池(由两个半径相等的圆组成).
(1)有人建议改为图②所示的形状,且图②中最外侧圆的直径与图①中一个圆的直径相同,只是担心原来备好的材料不够,请你比较这两种方案,哪一种方案所用材料多(即判断哪个周长更长)？
两种方案所用材料一样多。设题图①中一个圆的直径为d,周长为l,题图②中三个小圆的直径分别是d₁,d₂,d₃,周长分别是l₁,l₂,l₃,则l=πd=π(d₁+d₂+d₃)=πd₁+πd₂+πd₃=l₁+l₂+l₃.∴题图①中一个圆的周长与题图②中三个小圆周长的和相等。
(2)若将三个小圆改成n(n为正整数)个小圆,结论是否还成立？请说明理由.
成立。理由如下:设题图①中一个圆的直径为d,周长为l,n个小圆的直径分别是d₁,d₂,…,dₙ,周长分别是l₁,l₂,…,lₙ,则l=πd=π(d₁+d₂+…+dₙ)=πd₁+πd₂+…+πdₙ=l₁+l₂+…+lₙ,∴题图①中一个圆的周长与n(n为正整数)个小圆周长的和相等。

答案： 解:
(1)设题图①中一个圆的直径为d,周长为l,题图②中三个小圆的直径分别是d₁,d₂,d₃,周长分别是l₁,l₂,l₃,则l=πd=π(d₁+d₂+d₃)=πd₁+πd₂+πd₃=l₁+l₂+l₃.
∴题图①中一个圆的周长与题图②中三个小圆周长的和相等,即两种方案所用材料一样多.
(2)将三个小圆改成n(n为正整数)个小圆,结论仍成立.
理由如下:设题图①中一个圆的直径为d,周长为l,n个小圆的直径分别是d₁,d₂,…,dₙ,周长分别是l₁,l₂,…,lₙ,则l=πd=π(d₁+d₂+…+dₙ)=πd₁+πd₂+…+πdₙ=l₁+l₂+…+lₙ,
∴题图①中一个圆的周长与n(n为正整数)个小圆周长的和相等,即两种方案所用材料一样多.