《2025年全品学练考九年级数学上册苏科版江苏专版》

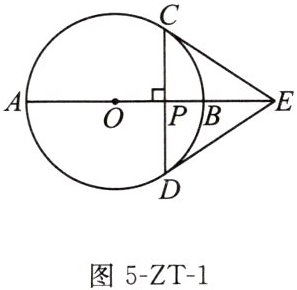
1. 如图5-ZT-1,在$\odot O$中,AB是直径,CD是弦,$AB⊥CD$,垂足为P,过点D作$\odot O$的切线与AB的延长线交于点E,连接CE.求证:CE为$\odot O$的切线.

证明：连接OC、OD，由DE是切线得∠ODE=90°，垂径定理得EC=ED，OC=OD，通过角度转化得∠OCE=90°，故CE为⊙O的切线

答案： 【解析】：连接$OC$、$OD$。
因为$DE$是$\odot O$的切线，所以$\angle ODE = 90^{\circ}$，即$\angle ODC+\angle CDE = 90^{\circ}$。
因为$AB$是直径，$AB\perp CD$，根据垂径定理可知$AB$垂直平分$CD$，所以$EC = ED$，则$\angle ECD=\angle EDC$。
又因为$OC = OD$，所以$\angle OCD=\angle ODC$。
那么$\angle OCD+\angle ECD=\angle ODC+\angle EDC = 90^{\circ}$，即$\angle OCE = 90^{\circ}$。
因为$OC$是$\odot O$的半径，且$OC\perp CE$，所以$CE$为$\odot O$的切线。
【答案】：连接$OC$、$OD$，由$DE$是切线得$\angle ODE = 90^{\circ}$，垂径定理得$EC = ED$，$OC = OD$，通过角度转化得$\angle OCE = 90^{\circ}$，故$CE$为$\odot O$的切线。

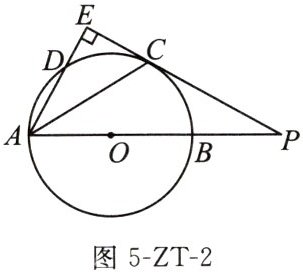
2. 如图5-ZT-2,$Rt△APE$中,$∠AEP= 90^{\circ }$,以AB为直径的$\odot O$交PE于点C,交AE于点D,且AC平分$∠EAP$.求证:PE是$\odot O$的切线.

证明:连接OC。
因为$OA = OC$，所以$\angle OAC=\angle OCA$。
又因为AC平分$\angle EAP$，所以$\angle OAC=\angle EAC$。
则$\angle OCA=\angle EAC$，所以OC//AE。
因为$\angle AEP = 90^{\circ}$，即$AE\perp PE$，根据两直线平行，同位角相等，可得$\angle OCP=\angle AEP = 90^{\circ}$，即OC⊥PE。
又因为OC是$\odot O$的半径，根据圆的切线判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线，所以PE是$\odot O$的切线。

答案： 【解析】：连接$OC$。
因为$OA = OC$，所以$\angle OAC=\angle OCA$。
又因为$AC$平分$\angle EAP$，所以$\angle OAC=\angle EAC$。
则$\angle OCA=\angle EAC$，所以$OC// AE$。
因为$\angle AEP = 90^{\circ}$，即$AE\perp PE$，根据两直线平行，同位角相等，可得$\angle OCP=\angle AEP = 90^{\circ}$，即$OC\perp PE$。
又因为$OC$是$\odot O$的半径，根据圆的切线判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线，所以$PE$是$\odot O$的切线。
【答案】：连接$OC$，通过证明$OC// AE$，得出$OC\perp PE$，再根据切线判定定理，证得$PE$是$\odot O$的切线。

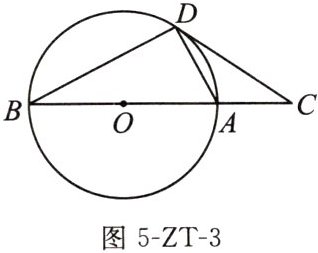
3. 如图5-ZT-3,D为$\odot O$上一点,C是直径BA延长线上的一点,连接CD,且$∠CDA= ∠CBD$.求证:CD是$\odot O$的切线.

证明:连接$OD$，$\because OB = OD$，$\therefore\angle OBD=\angle ODB$，$\because\angle CDA=\angle CBD$，$\therefore\angle CDA=\angle ODB$。
$\because AB$是直径，$\therefore\angle BDA = 90^{\circ}$，即$\angle ODB+\angle ODA=90^{\circ}$，$\therefore\angle CDA+\angle ODA = 90^{\circ}$，$\angle ODC = 90^{\circ}$。
$\because OD$是半径，$OD\perp CD$，$\therefore CD$是$\odot O$的切线。

答案： 【解析】：
连接$OD$，因为$OB = OD$，所以$\angle OBD=\angle ODB$（等边对等角）。
又因为$\angle CDA=\angle CBD$，所以$\angle CDA=\angle ODB$。
因为$AB$是$\odot O$的直径，所以$\angle BDA = 90^{\circ}$（直径所对的圆周角是直角），即$\angle ODB+\angle ODA=90^{\circ}$。
把$\angle CDA=\angle ODB$代入可得$\angle CDA+\angle ODA = 90^{\circ}$，即$\angle ODC=90^{\circ}$。
因为$OD$是$\odot O$的半径，且$OD\perp CD$，根据切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线，所以$CD$是$\odot O$的切线。
【答案】：
连接$OD$，$\because OB = OD$，$\therefore\angle OBD=\angle ODB$，$\because\angle CDA=\angle CBD$，$\therefore\angle CDA=\angle ODB$。
$\because AB$是直径，$\therefore\angle BDA = 90^{\circ}$，即$\angle ODB+\angle ODA=90^{\circ}$，$\therefore\angle CDA+\angle ODA = 90^{\circ}$，$\angle ODC = 90^{\circ}$。
$\because OD$是半径，$OD\perp CD$，$\therefore CD$是$\odot O$的切线。

4. 已知$\odot O$与正方形ABCD如图5-ZT-4放置,点A,B,M在$\odot O$上,连接DM.已知$\odot O$的半径为5,$DM= 4\sqrt {7},AB= 8$.求证:DM是$\odot O$的切线.

答案：
证明:过点O作OH⊥CD于点H,交AB于点E,连接OM,OD,OB,如图.

∵AB//CD,
∴OE⊥AB,
∴AE=BE=4.
在Rt△OBE中,OE = $\sqrt{OB^{2}-BE^{2}}=\sqrt{5^{2}-4^{2}} = 3$.
∵四边形ABCD为正方形，
∴CD=AB=AD=8,∠BAD=∠ADC = 90°.
∵∠BAD=∠ADC=∠EHD=90°,
∴四边形AEHD为矩形，
∴DH=AE=4,EH=AD=8,
∴OH=OE+EH=3+8=11.
在Rt△OHD中,
∵DH=4,OH=11,
∴OD = $\sqrt{4^{2}+11^{2}}=\sqrt{137}$
∵OM=5,DM = $4\sqrt{7}$,OD = $\sqrt{137}$,
∴$OM^{2}+DM^{2}=OD^{2}$,
∴△OMD为直角三角形，∠OMD=90°,
∴OM⊥DM.
又
∵OM为⊙O的半径，
∴DM是⊙O的切线.

5. 如图5-ZT-5,BD是$∠ABC$的平分线,O是BD上一点,$\odot O$与AB相切于点M,与BD交于点E,F.求证:BC是$\odot O$的切线.


证明：连接$OM$，过$O$作$ON\perp BC$于$N$。
$\because AB$切$\odot O$于$M$，$\therefore OM\perp AB$。
$\because BD$平分$\angle ABC$，$OM\perp AB$，$ON\perp BC$，$\therefore OM = ON$。
$\because ON\perp BC$且$ON$是$\odot O$半径，$\therefore BC$是$\odot O$的切线。

答案： 【解析】：
连接$OM$，过点$O$作$ON\perp BC$于点$N$。
因为$AB$是$\odot O$的切线，所以$OM\perp AB$。
又因为$BD$是$\angle ABC$的平分线，根据角平分线的性质：角平分线上的点到角两边的距离相等，可得$OM = ON$。
因为$ON\perp BC$，$ON$是$\odot O$的半径，所以$BC$是$\odot O$的切线（经过半径的外端并且垂直于这条半径的直线是圆的切线）。
【答案】：
连接$OM$，过$O$作$ON\perp BC$于$N$。
$\because AB$切$\odot O$于$M$，$\therefore OM\perp AB$。
$\because BD$平分$\angle ABC$，$OM\perp AB$，$ON\perp BC$，$\therefore OM = ON$。
$\because ON\perp BC$且$ON$是$\odot O$半径，$\therefore BC$是$\odot O$的切线。