第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 如图2-2-11,已知$\odot O的直径AB⊥CD$于点E,则下列结论不一定成立的是(
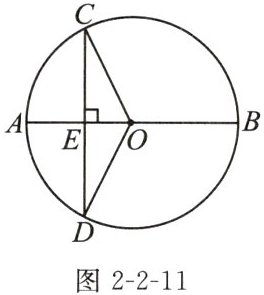
A. $CE= DE$
B. $AE= OE$
C. $\overset{\frown }{BC}= \overset{\frown }{BD}$
D. $\overset{\frown }{AC}= \overset{\frown }{AD}$
B
)
A. $CE= DE$
B. $AE= OE$
C. $\overset{\frown }{BC}= \overset{\frown }{BD}$
D. $\overset{\frown }{AC}= \overset{\frown }{AD}$
答案:
B
2. 如图2-2-12,$\odot O$的半径为5,弦$AB= 8$,$OC⊥AB$于点C,则OC的长为(
A. 1
B. 2
C. 3
D. 4
C
)A. 1
B. 2
C. 3
D. 4
答案:
C
3. 如图2-2-13,AB是$\odot O$的弦,半径$OC⊥AB$,垂足为D,$\odot O$的半径为5,$CD= 1$,则AB的长为(

A. 4
B. 6
C. 8
D. 10
B
)
A. 4
B. 6
C. 8
D. 10
答案:
B
4. (2023无锡月考)如图2-2-14,AB是$\odot O$的直径,弦$CD⊥AB$于点E,$BE= 2$,$CD= 8$,则$\odot O$的半径为(
A. 2
B. 3
C. 5
D. 8
C
)A. 2
B. 3
C. 5
D. 8
答案:
C
5. 如图2-2-15,在平面直角坐标系中,点$O'$在x轴上,$\odot O'$与两坐标轴分别交于A,C,B,D四点,已知$A(6,0)$,$C(-2,0)$,则点D的坐标为______
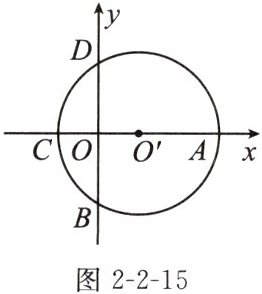
(0,2$\sqrt{3}$)
.
答案:
(0,2$\sqrt{3}$)
6. 如图2-2-16,$∠C= 90^{\circ }$,$\odot C$与AB相交于点A,D,$AC= 6$,$CB= 8$,则AD的长为______
$\frac{36}{5}$
.
答案:
$\frac{36}{5}$
7. (2024扬州月考)《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有圆材埋壁中,不知大小.以锯锯之,深1寸,锯道长1尺,问径几何?”其意思为“如图2-2-17,今有一圆形木材($\odot O$)埋在墙中,不知其大小,用锯子去锯这根木材,锯口深$DE= 1$寸,锯道长$AB= 10$寸,问这根圆形木材的截面直径CD是多少?”请解答此问题.
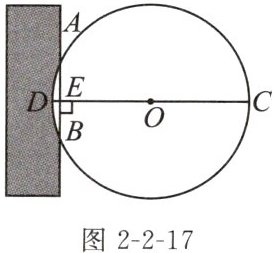
答:这根圆形木材的截面直径CD是

答:这根圆形木材的截面直径CD是
26寸
.
答案:
26寸
8. (2024连云港期中)如图2-2-18,$\odot O$的直径AB垂直于弦CD,垂足为E,$∠A= 30^{\circ }$,$\odot O$的半径为2,则弦CD的长为(
A. 2
B. $2\sqrt {3}$
C. $\sqrt {3}$
D. 4
B
)A. 2
B. $2\sqrt {3}$
C. $\sqrt {3}$
D. 4
答案:
B
9. (2023南通期中)如图2-2-19,CD是$\odot O$的直径,弦$AB= 8cm$,$AB⊥CD$,垂足为M,$OM:OC= 3:5$,则直径CD的长为(
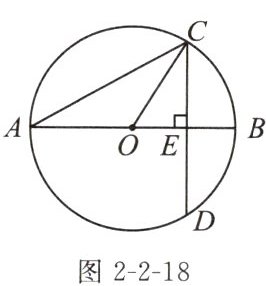
A. $2\sqrt {7}cm$
B. $\sqrt {7}cm$
C. 10cm
D. 5cm
C
)
A. $2\sqrt {7}cm$
B. $\sqrt {7}cm$
C. 10cm
D. 5cm
答案:
C
查看更多完整答案,请扫码查看


