《2025年全品学练考九年级数学上册苏科版江苏专版》

1. 下列直线中,一定是圆的切线的是 (C)
A. 与圆有公共点的直线
B. 垂直于圆的半径的直线
C. 过圆上一点且与以这点为端点的半径垂直的直线
D. 经过圆的直径一端的直线

答案： C

2. 如图2-5-9,AB是$\odot O$的直径,BC是$\odot O$的切线.若$∠BAC= 35^{\circ }$,则$∠ACB$的大小为 (C)

A.$35^{\circ }$
B.$45^{\circ }$
C.$55^{\circ }$
D.$65^{\circ }$

答案： C

3. (2023连云港期末)如图2-5-10,AB是$\odot O$的切线,切点为B,连接AO与$\odot O$交于点C,D为$\widehat {BmC}$上一点,连接BD,CD.若$∠A= 36^{\circ }$,则$∠BDC$的度数为 (C)
A.$32^{\circ }$
B.$18^{\circ }$
C.$27^{\circ }$
D.$36^{\circ }$

答案： C

4. (2023徐州期中)如图2-5-11,P为$\odot O$外一点,PT与$\odot O$相切于点T,$OP= 10,∠OPT= 30^{\circ }$,则$\odot O$的半径为______5.

答案： 5

5. 如图2-5-12,AB是$\odot O$的直径,AC切$\odot O$于点A,BC交$\odot O$于点D.若$∠C= 70^{\circ }$,则$∠AOD$的度数为______40$^{\circ }$.

答案： 40

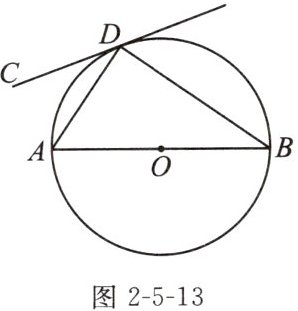
6. (2023攀枝花)如图2-5-13,AB为$\odot O$的直径,如果圆上的点D恰使$∠ADC= ∠B$,求证:直线CD与$\odot O$相切.

连接$OD$，因为$AB$是$\odot O$直径，所以$\angle ADB = 90^{\circ}$，$OB = OD$得$\angle B=\angle ODB$，又$\angle ADC=\angle B$，所以$\angle ADC=\angle ODB$，进而$\angle ODC = 90^{\circ}$，$OD$是半径且$OD\perp CD$，所以直线$CD$与$\odot O$相切。

答案： 【解析】：
连接$OD$。
因为$AB$是$\odot O$的直径，所以$\angle ADB = 90^{\circ}$，即$\angle ADO+\angle ODB = 90^{\circ}$。
因为$OB = OD$，所以$\angle B=\angle ODB$。
又因为$\angle ADC=\angle B$，所以$\angle ADC=\angle ODB$。
那么$\angle ADC+\angle ADO = 90^{\circ}$，即$\angle ODC = 90^{\circ}$。
因为$OD$是$\odot O$的半径，且$OD\perp CD$，根据圆的切线判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线，所以直线$CD$与$\odot O$相切。
【答案】：
连接$OD$，因为$AB$是$\odot O$直径，所以$\angle ADB = 90^{\circ}$，$OB = OD$得$\angle B=\angle ODB$，又$\angle ADC=\angle B$，所以$\angle ADC=\angle ODB$，进而$\angle ODC = 90^{\circ}$，$OD$是半径且$OD\perp CD$，所以直线$CD$与$\odot O$相切。

7. (2023常州期中)如图2-5-14,以AB为直径的$\odot O$上有C,D两点,过点C作$\odot O$的切线CE,连接AD并延长交CE于点E,连接AC,AC平分$∠BAD$.
(1)求证:$∠AEC= 90^{\circ }$;
(2)若$AD= 6,CE= 2$,求$\odot O$的半径.$\sqrt{13}$

答案：
(1)略
(2)$\sqrt{13}$