第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
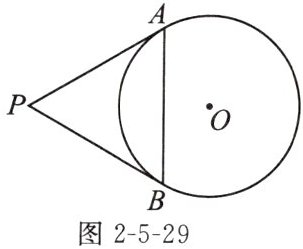
1. 如图2-5-29,从$\odot O$外一点P引$\odot O$的两条切线PA,PB,切点分别为A,B.如果$∠APB= 60^{\circ }$,$PA= 8$,那么弦AB的长是(
A. 4
B. 8
C. $4\sqrt {3}$
D. $8\sqrt {3}$
B
)
A. 4
B. 8
C. $4\sqrt {3}$
D. $8\sqrt {3}$
答案:
B
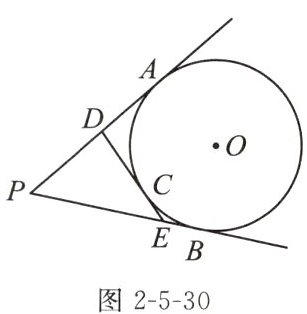
2.(2023扬州期中)如图2-5-30,PA,PB分别切$\odot O$于点A,B,过$\odot O$上一点C的切线分别交PA,PB于点D,E.若$PA= 6cm$,则$\triangle PDE$的周长为______
12
cm.
答案:
12
3. 如图2-5-31,在$\triangle ABC$中,$∠A= 60^{\circ }$,$BC= 6$,它的周长为16.若$\odot O$与BC,AC,AB三边分别切于点E,F,D,则DF的长为______
2
.
答案:
2
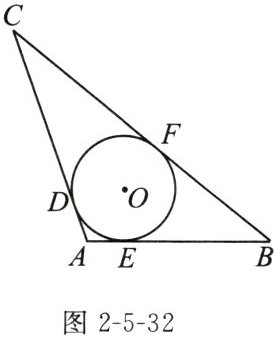
4. 如图2-5-32,$\triangle ABC的内切圆\odot O$与AC,AB,BC分别相切于点D,E,F,且$AB= 5cm$,$BC= 9cm$,$AC= 6cm$,求AE=
1 cm
,BF=4 cm
和CD=5 cm
的长.
答案:
解:设$AE = x$ $cm$,$BF = y$ $cm$,$CD = z$ $cm$。
因为$\odot O$是$\triangle ABC$的内切圆,$\odot O$与$AC$,$AB$,$BC$分别相切于点$D$,$E$,$F$,根据切线长定理可知:$AE = AD = x$ $cm$,$BE = BF = y$ $cm$,$CD = CF = z$ $cm$。
已知$AB = 5$ $cm$,$BC = 9$ $cm$,$AC = 6$ $cm$,则可得方程组:
$\begin{cases}x + y = 5\\y + z = 9\\x + z = 6\end{cases}$
将三个方程相加得:$2(x + y + z)=5 + 9 + 6$,即$2(x + y + z)=20$,所以$x + y + z = 10$。
用$x + y + z = 10$分别减去方程组中的三个方程:
$z=(x + y + z)-(x + y)=10 - 5 = 5$;
$x=(x + y + z)-(y + z)=10 - 9 = 1$;
$y=(x + y + z)-(x + z)=10 - 6 = 4$。
所以$AE = 1$ $cm$,$BF = 4$ $cm$,$CD = 5$ $cm$。
因为$\odot O$是$\triangle ABC$的内切圆,$\odot O$与$AC$,$AB$,$BC$分别相切于点$D$,$E$,$F$,根据切线长定理可知:$AE = AD = x$ $cm$,$BE = BF = y$ $cm$,$CD = CF = z$ $cm$。
已知$AB = 5$ $cm$,$BC = 9$ $cm$,$AC = 6$ $cm$,则可得方程组:
$\begin{cases}x + y = 5\\y + z = 9\\x + z = 6\end{cases}$
将三个方程相加得:$2(x + y + z)=5 + 9 + 6$,即$2(x + y + z)=20$,所以$x + y + z = 10$。
用$x + y + z = 10$分别减去方程组中的三个方程:
$z=(x + y + z)-(x + y)=10 - 5 = 5$;
$x=(x + y + z)-(y + z)=10 - 9 = 1$;
$y=(x + y + z)-(x + z)=10 - 6 = 4$。
所以$AE = 1$ $cm$,$BF = 4$ $cm$,$CD = 5$ $cm$。
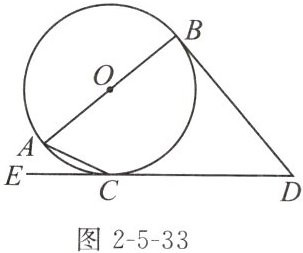
5.(2024无锡月考)如图2-5-33,AB是$\odot O$的直径,DB,DE分别切$\odot O$于点B,C.若$∠ACE= 25^{\circ }$,则$∠D$的度数是(
A. $50^{\circ }$
B. $55^{\circ }$
C. $60^{\circ }$
D. $65^{\circ }$
A
)
A. $50^{\circ }$
B. $55^{\circ }$
C. $60^{\circ }$
D. $65^{\circ }$
答案:
A
6. 如图2-5-34,PA,PB是$\odot O$的切线,A,B为切点,点C,D在$\odot O$上.若$∠P= 102^{\circ }$,则$∠A+∠C= $
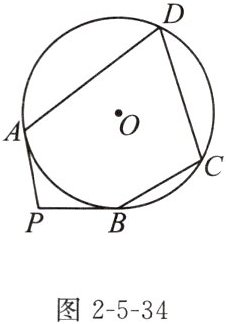
219
$^{\circ }$.
答案:
219
7.(2023盐城亭湖区期末)如图2-5-35,$\triangle ABC$是一张周长为17cm的三角形纸片,$BC= 5cm$,$\odot O$是它的内切圆,小明准备用剪刀在$\odot O$的右侧沿着与$\odot O$相切的任意一条直线MN剪下$\triangle AMN$,则剪下的$\triangle AMN$的周长为______
7 cm
.
答案:
$ 7 \text{ cm} $
8. 如图2-5-36所示,AB是$\odot O$的直径,AD和BC分别切$\odot O$于A,B两点,CD与$\odot O$有公共点E,且$AD= DE$.
(1)求证:CD是$\odot O$的切线;
(2)若$AB= 12$,$BC= 4$,则AD的长为______
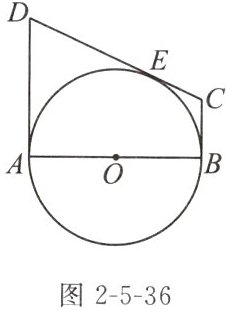
(1)求证:CD是$\odot O$的切线;
(2)若$AB= 12$,$BC= 4$,则AD的长为______
9
.
答案:
(1)略
(2)9
(1)略
(2)9
查看更多完整答案,请扫码查看


