《2025年全品学练考九年级数学上册苏科版江苏专版》

1. (2024苏州期中)两个连续正整数的平方和为113,则这两个数的积是____56.

答案： 56

2. 某中学九年级(6)班学生毕业时,每个同学都要给其他同学写一份毕业留言留作纪念,全班学生共写了930份留言.如果设全班有x名学生,根据题意,列出方程为 (B)
A. $x(x+1)= 930$
B. $x(x-1)= 930$
C. $\frac{x(x-1)}{2}= 930$
D. $\frac{x(x+1)}{2}= 930$

答案： B

3. (2024湖州期末)一次围棋比赛采用单循环赛制(即每位选手与其他选手各比赛1局),且参赛者少于15人.小珺和小哲对比赛的总局数进行的统计如图3-ZT-1:

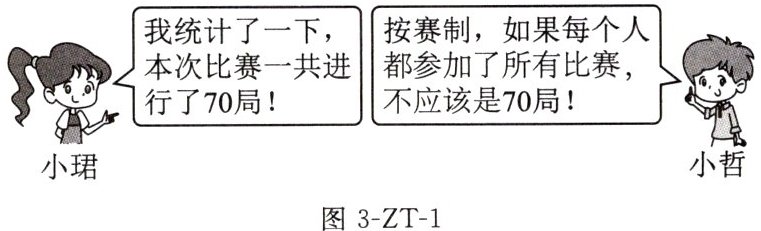
(1)若参赛者共5人,按赛制应该进行10局比赛?
(2)小哲说的有道理吗?请通过计算说明;小哲说的有道理.说明略
(3)他们经过查询,小珺的统计无误,是有一人中途退出比赛,请直接写出报名本次比赛的人数.13 人

答案：
(1)10 局
(2)小哲说的有道理.说明略
(3)13 人

4. (2024南通期末)某商场销售一种成本为20元/kg的商品,市场调研反映:在某个月的第x天$(1≤x≤30)的销售价格为(40+x)$元/kg,日销售量$y(kg)$与x的函数关系如图3-ZT-2所示.
(1)y与x的函数表达式为$y=-2x+100$;
(2)销售该商品第几天时,日销售利润为2250元?第 5 天或第 25 天
(3)日销售利润能达到2500元吗?说明理由.日销售利润不能达到 2500 元.理由略

图3-ZT-2

答案：
(1)$y=-2x+100$
(2)第 5 天或第 25 天
(3)日销售利润不能达到 2500 元.理由略

5. 新情境数学文化《九章算术》是我国古代数学名著,记载着这样一个问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”大意是:有一个池塘,其底面是一个边长为10尺的正方形,在池塘正中央有一棵芦苇,它高出水面1尺.如果把这棵芦苇沿与水池边垂直的方向拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这棵芦苇的长度分别是多少?设芦苇的长度为x尺,则可列方程为 (C)
A. $x^{2}+5^{2}= (x+1)^{2}$
B. $x^{2}+10^{2}= (x+1)^{2}$
C. $x^{2}-5^{2}= (x-1)^{2}$
D. $x^{2}-10^{2}= (x-1)^{2}$

答案： C

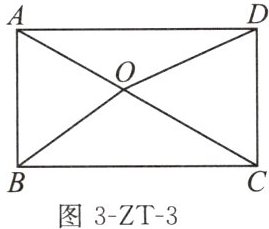
6. 如图3-ZT-3,O是矩形ABCD内一点,且点O到四个顶点的距离OA,OB,OC,OD满足关系式$OA^{2}+OC^{2}= OB^{2}+OD^{2}$,若点O在对角线AC上,$AC= 4$,$OB= \frac{\sqrt{13}}{2}$,$OD= \frac{\sqrt{21}}{2}$,则$OA=$$\frac {3}{2}$或$\frac {5}{2}$.
图3-ZT-3

答案： $\frac {3}{2}$或$\frac {5}{2}$