第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
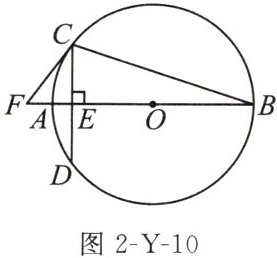
10. (2024 宿迁改编)如图 2-Y-10,在$\odot O$中,AB 是直径,CD 是弦,且$AB⊥CD$,垂足为 E,在 BA 的延长线上取一点 F,连接 CF,使$∠FCD= 2∠B$.
求证:CF 是$\odot O$的切线.
求证:CF 是$\odot O$的切线.

答案:
证明:如图,连接 OC.

$\because OC=OB,\therefore ∠B=∠BCO,$
$\therefore ∠AOC=∠B+∠BCO=2∠B.$
$\because AB⊥CD,\therefore ∠CEO=90^{\circ },$
$\therefore ∠COE+∠OCE=90^{\circ }.$
$\because ∠FCD=2∠B,\therefore ∠FCD=∠COE,$
$\therefore ∠FCD+∠OCE=90^{\circ },$
$\therefore ∠OCF=90^{\circ }$,即$OC⊥CF.$
又
∵OC是$\odot O$的半径,
∴CF是$\odot O$的切线.
证明:如图,连接 OC.

$\because OC=OB,\therefore ∠B=∠BCO,$
$\therefore ∠AOC=∠B+∠BCO=2∠B.$
$\because AB⊥CD,\therefore ∠CEO=90^{\circ },$
$\therefore ∠COE+∠OCE=90^{\circ }.$
$\because ∠FCD=2∠B,\therefore ∠FCD=∠COE,$
$\therefore ∠FCD+∠OCE=90^{\circ },$
$\therefore ∠OCF=90^{\circ }$,即$OC⊥CF.$
又
∵OC是$\odot O$的半径,
∴CF是$\odot O$的切线.
11. (2024 连云港)【问题情境】
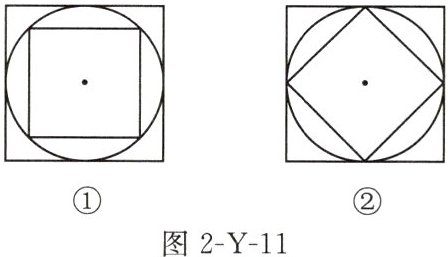
(1)如图 2-Y-11①,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面积的几倍? 小昕将小正方形绕圆心旋转$45^{\circ }$(如图②),这时候就容易发现大正方形面积是小正方形面积的______倍.由此可见,图形变化是解决问题的有效策略.
【操作实践】
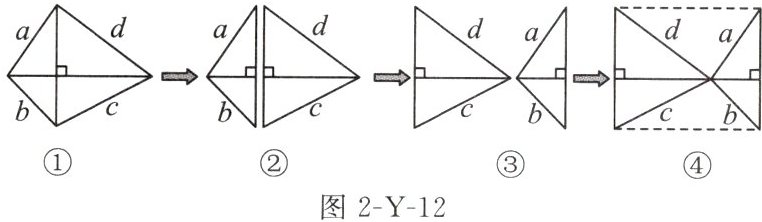
(2)如图 2-Y-12①是一个对角线互相垂直的四边形,四条边长 a,b,c,d 之间存在某种数量关系.小昕按图中所示步骤进行操作,并将最终图形抽象成图 2-Y-13.请你结合整个变化过程,直接写出图 2-Y-13 中以矩形内一
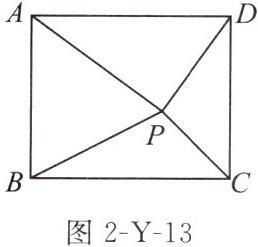
点 P 为端点的四条线段之间的数量关系;
【探究应用】
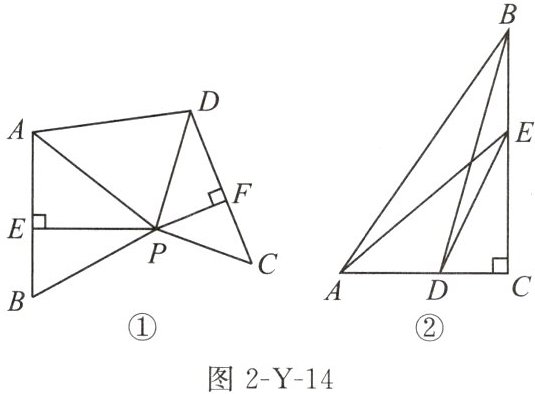
(3)如图 2-Y-14①,在图 2-Y-12 中“④”的基础上,小昕将$△PDC$绕点 P 逆时针旋转,他发现旋转过程中$∠DAP$存在最大值.若$PE= 8,PF= 5$,当$∠DAP$最大时,求 AD 的长;
(4)如图②,在$Rt△ABC$中,$∠C= 90^{\circ }$,点 D,E 分别在边 AC 和 BC 上,连接 DE,AE,BD.若$AC+CD= 5,BC+CE= 8$,求$AE+BD$的最小值.
(1)如图 2-Y-11①,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面积的几倍? 小昕将小正方形绕圆心旋转$45^{\circ }$(如图②),这时候就容易发现大正方形面积是小正方形面积的______倍.由此可见,图形变化是解决问题的有效策略.

【操作实践】
(2)如图 2-Y-12①是一个对角线互相垂直的四边形,四条边长 a,b,c,d 之间存在某种数量关系.小昕按图中所示步骤进行操作,并将最终图形抽象成图 2-Y-13.请你结合整个变化过程,直接写出图 2-Y-13 中以矩形内一

点 P 为端点的四条线段之间的数量关系;

【探究应用】
(3)如图 2-Y-14①,在图 2-Y-12 中“④”的基础上,小昕将$△PDC$绕点 P 逆时针旋转,他发现旋转过程中$∠DAP$存在最大值.若$PE= 8,PF= 5$,当$∠DAP$最大时,求 AD 的长;
(4)如图②,在$Rt△ABC$中,$∠C= 90^{\circ }$,点 D,E 分别在边 AC 和 BC 上,连接 DE,AE,BD.若$AC+CD= 5,BC+CE= 8$,求$AE+BD$的最小值.

答案:
解:
(1)2
(2)$PA^{2}+PC^{2}=PB^{2}+PD^{2}.$
(3)$\because$将$\triangle PDC$绕点 P 逆时针旋转,
$\therefore$点 D 在以点 P 为圆心,PD 为半径的圆上,如图①.

$\because$A 为圆外一个定点,
$\therefore$当 AD 与$\odot P$相切时,$∠DAP$最大,
$\therefore PD⊥AD,\therefore AD^{2}=AP^{2}-PD^{2}.$
易得$AE=DF.$
$\because PE=8,PF=5,$
$\therefore AD^{2}=AP^{2}-PD^{2}=PE^{2}+AE^{2}-PF^{2}-DF^{2}=8^{2}-5^{2}=39,$
$\therefore AD=\sqrt{39}.$
(4)如图②,作$\triangle BDC$关于 BC 对称的$\triangle BCD_{1},\triangle AEC$关于 AC 对称的$\triangle AE_{1}C$,连接$D_{1}E_{1},$

$\therefore CD=CD_{1},CE=CE_{1}.$
再将$\triangle ABE_{1}$沿 AC 方向平移,使点 A 与点$D_{1}$重合,如图③,得到$\triangle D_{1}B_{1}E_{2}$,连接$E_{1}E_{2},BE_{2}$,则$∠BE_{1}E_{2}=90^{\circ }.$

由轴对称及平移的性质可得$AE+BD=D_{1}E_{2}+BD_{1},$
$\therefore$当$E_{2},D_{1}$,B 三点共线时,$AE+BD$的值最小,最小值为$BE_{2}$的长.
$\because AC+CD=5,BC+CE=8,$
$\therefore E_{1}E_{2}=5,BE_{1}=8,$
$\therefore BE_{2}=\sqrt{BE_{1}^{2}+E_{1}E_{2}^{2}}=\sqrt{8^{2}+5^{2}}=\sqrt{89},$
$\therefore AE+BD$的最小值为$\sqrt{89}.$
解:
(1)2
(2)$PA^{2}+PC^{2}=PB^{2}+PD^{2}.$
(3)$\because$将$\triangle PDC$绕点 P 逆时针旋转,
$\therefore$点 D 在以点 P 为圆心,PD 为半径的圆上,如图①.

$\because$A 为圆外一个定点,
$\therefore$当 AD 与$\odot P$相切时,$∠DAP$最大,
$\therefore PD⊥AD,\therefore AD^{2}=AP^{2}-PD^{2}.$
易得$AE=DF.$
$\because PE=8,PF=5,$
$\therefore AD^{2}=AP^{2}-PD^{2}=PE^{2}+AE^{2}-PF^{2}-DF^{2}=8^{2}-5^{2}=39,$
$\therefore AD=\sqrt{39}.$
(4)如图②,作$\triangle BDC$关于 BC 对称的$\triangle BCD_{1},\triangle AEC$关于 AC 对称的$\triangle AE_{1}C$,连接$D_{1}E_{1},$

$\therefore CD=CD_{1},CE=CE_{1}.$
再将$\triangle ABE_{1}$沿 AC 方向平移,使点 A 与点$D_{1}$重合,如图③,得到$\triangle D_{1}B_{1}E_{2}$,连接$E_{1}E_{2},BE_{2}$,则$∠BE_{1}E_{2}=90^{\circ }.$

由轴对称及平移的性质可得$AE+BD=D_{1}E_{2}+BD_{1},$
$\therefore$当$E_{2},D_{1}$,B 三点共线时,$AE+BD$的值最小,最小值为$BE_{2}$的长.
$\because AC+CD=5,BC+CE=8,$
$\therefore E_{1}E_{2}=5,BE_{1}=8,$
$\therefore BE_{2}=\sqrt{BE_{1}^{2}+E_{1}E_{2}^{2}}=\sqrt{8^{2}+5^{2}}=\sqrt{89},$
$\therefore AE+BD$的最小值为$\sqrt{89}.$
查看更多完整答案,请扫码查看


