第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1. 如图2-5-19,$\odot O是\triangle ABC$的内切圆,则O是$\triangle ABC$的(
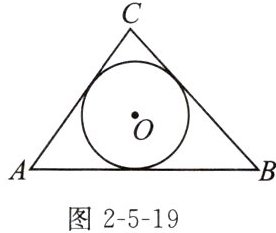
A. 三条边的垂直平分线的交点
B. 三条角平分线的交点
C. 三条中线的交点
D. 三条高的交点
B
)
A. 三条边的垂直平分线的交点
B. 三条角平分线的交点
C. 三条中线的交点
D. 三条高的交点
答案:
B
2. 如图2-5-20,点O是$\triangle ABC$的内切圆的圆心.若$∠BAC= 80^{\circ }$,则$∠BOC$的度数为(
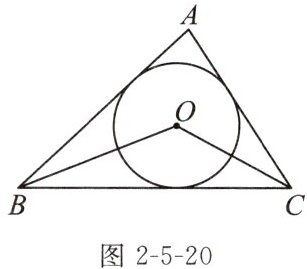
A. $100^{\circ }$
B. $110^{\circ }$
C. $120^{\circ }$
D. $130^{\circ }$
D
)
A. $100^{\circ }$
B. $110^{\circ }$
C. $120^{\circ }$
D. $130^{\circ }$
答案:
D
3. 如图2-5-21,已知$\triangle ABC的面积为18cm^{2}$,其周长为24 cm,则$\triangle ABC$内切圆的半径为(
A. 1 cm
B. $\frac {3}{2}cm$
C. 2 cm
D. $\frac {3}{4}cm$
B
)A. 1 cm
B. $\frac {3}{2}cm$
C. 2 cm
D. $\frac {3}{4}cm$
答案:
B
4. 直角三角形的两条直角边长分别是5和12,则它的内切圆的半径为
2
.
答案:
2
5. 已知:如图2-5-22,$\triangle ABC$.
求作:$\triangle ABC的内切圆\odot P$.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)
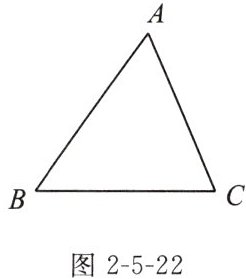
求作:$\triangle ABC的内切圆\odot P$.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)

答案:
解:如图,⊙P 即为所求作的圆.

解:如图,⊙P 即为所求作的圆.

6. 如图2-5-23,在$\triangle ABC$中,点E是内心,延长AE交$\triangle ABC$的外接圆于点D,连接BD,CD,CE,BE,且$∠BDA= 60^{\circ }$.
(1)求证:$\triangle BDE$是等边三角形;
(2)若$∠BDC= 120^{\circ }$,猜想四边形BDCE是怎样的四边形,并证明你的猜想.
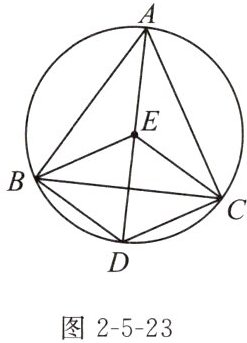
(1)
(2)猜想:四边形BDCE是
(1)求证:$\triangle BDE$是等边三角形;
(2)若$∠BDC= 120^{\circ }$,猜想四边形BDCE是怎样的四边形,并证明你的猜想.

(1)
证明:∵点E是△ABC的内心,∴AE平分∠BAC,BE平分∠ABC,∴∠BAD=∠CAD,∠ABE=∠CBE.∵∠BDA=60°,∠CAD=∠CBD,∴∠BAD=∠CBD,∴∠BDE=∠BAD+∠ABE=∠CBD+∠CBE=∠DBE,∴∠BDE=∠DBE=60°,∴△BDE是等边三角形.
(2)猜想:四边形BDCE是
菱形
.证明:∵∠BDC=120°,∠BDA=60°,∴∠ADC=∠BDC - ∠BDA=60°,同理可证△CDE是等边三角形,∴DE=DC=CE.∵△BDE是等边三角形,∴BD=DE=BE,∴BD=DC=CE=BE,∴四边形BDCE是菱形.
答案:
(1)略
(2)猜想:四边形 BDCE 是菱形.证明略
(1)略
(2)猜想:四边形 BDCE 是菱形.证明略
7. (2024徐州期中)根据圆规作图的痕迹,可用直尺成功找到三角形内心的图形是(
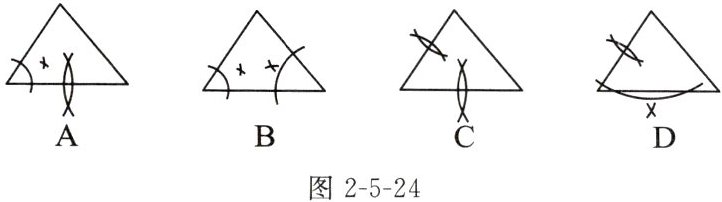
B
)
答案:
B
查看更多完整答案,请扫码查看


