《2025年全品学练考九年级数学上册苏科版江苏专版》

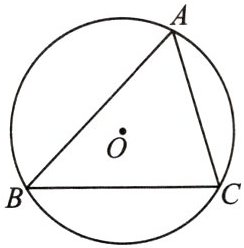
10. 如图2-4-25,$\odot O是\triangle ABC$的外接圆,$∠A= 60^{\circ }$,$BC= 4\sqrt {3}$,则$\odot O$的半径是______4。

答案： 4

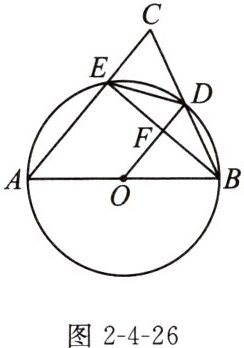
11. 如图2-4-26,在$\triangle ABC$中,$AB= AC$,以AB为直径的$\odot O$分别交BC,AC于点D,E,连接BE交OD于点F。
(1)求证：$OD⊥BE$；
(2)连接DE,若$DE= 2$,$AB= 5$,求AE的长。

答案：

(1)证明:连接AD,OE,如图,
　　　　　　
　
∵AB为⊙O的直径，
　
∴∠ADB = ∠ADC = 90°，
∴AD⊥BC.
　
∵AB = AC，
∴AD平分∠BAC,
　
∴∠CAD = ∠BAD，
∴$\overset{\frown }{BD}=\overset{\frown }{ED}$，
　
∴BD = ED，又OB = OE,
　
∴OD垂直平分BE，
∴OD⊥BE.
(2)$\frac{17}{5}$

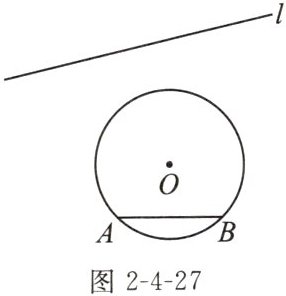
12. 新考法探究性如图2-4-27,已知AB是$\odot O$的一条弦,直线l与$\odot O$无交点,利用无刻度的直尺在直线l上找一点C,使得$\triangle ABC$为直角三角形。(无需写出画图步骤)

答案：
解:如图，连接BO并延长，交⊙O于点D,连接AD并延长，交直线l于点$C_{1}$，连接$BC_{1}$.
　
∵BD为⊙O的直径，
　
∴∠BAD = 90°，
　
∴△ABC₁为直角三角形，
　　则点$C_{1}$即为所求;
　　连接AO并延长，交⊙O于点E，连接BE并延长，交直线l于点$C_{2}$，连接$AC_{2}$.
　
∵AE为⊙O的直径，
　
∴∠ABE = 90°，
　
∴△ABC₂为直角三角形，
　　则点$C_{2}$即为所求.
　　综上，点$C_{1}$，$C_{2}$均满足题意.
　　　　　　　　　　　参考答案　　活15
　　　　　

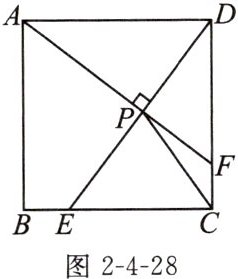
如图 2 - 4 - 28,E 是正方形 ABCD 的边 BC 上一动点(点 E 不与点 B,C 重合),连接 DE,过点 A 作 AF⊥DE 交 CD 于点 F,垂足为 P,连接 PC,已知正方形 ABCD 的边长为 2,则 PC 长的最小值为$\sqrt{5}-1$。

答案： $ \sqrt { 5 } - 1 $

1. (2023 扬州邗江区模拟)如图 2 - 4 - 29,直线 $ y = \frac{3}{4}x + 6 $ 分别与 x 轴、y 轴相交于点 M,N。点 P 在平面内,$ ∠MPN = 90° $,点 $ C(0,3) $,则 PC 长的最小值是______1。

答案： 1

2. $ Rt△ABC $ 中,$ AB⊥BC $,$ AB = 4 $,$ BC = 3 $,P 是 $ △ABC $ 内部的一个动点,满足 $ ∠PAB = ∠PBC $,则线段 CP 长的最小值为$ \sqrt { 13 } - 2 $。

答案： $ \sqrt { 13 } - 2 $