《2025年名校调研跟踪测试卷九年级数学下册人教版》

8. 如图是一个正六棱柱的主视图和左视图，则图中的$a$等于 ( )

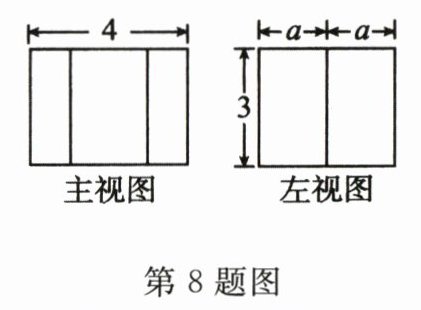
A. $2\sqrt{3}$
B. $\sqrt{3}$
C. 2
D. 1

答案： B

9. 我国某型号运载火箭的整流罩的三视图如图所示，根据图中数据(单位：m)可算出该整流罩的侧面积是 ( )

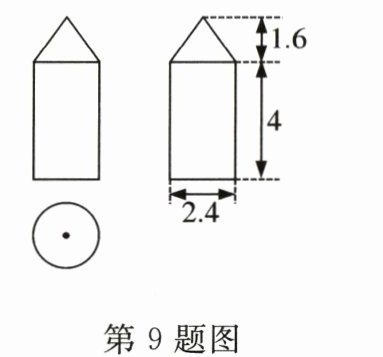
A. $13.44\pi\ m^{2}$
B. $12\pi\ m^{2}$
C. $11.52\pi\ m^{2}$
D. $7.2\pi\ m^{2}$

答案： B 【解析】由图知，该整流罩上面部分为圆锥，下面部分为圆柱，
圆锥的母线长$l = \sqrt{(\frac{2.4}{2})^{2}+1.6^{2}} = 2(m)$，
∴$S_{侧}=\pi\times2.4\times4+\frac{1}{2}\pi\times2.4\times2 = 12\pi(m^{2})$.
故选：B.

10. 图2是图1中长方体的三视图，若用$S$表示面积，且$S_{主视图}=x^{2}+2x$，$S_{左视图}=x^{2}+x$，则$S_{俯视图}$等于 ( )

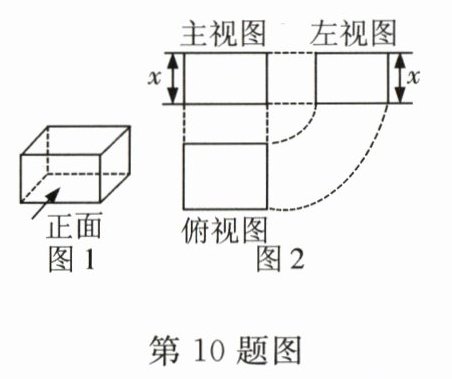
A. $x^{2}+4x + 3$
B. $2x^{2}+4x$
C. $x^{2}+2x + 1$
D. $x^{2}+3x + 2$

答案： D 【解析】
∵$S_{主视图}=x^{2}+2x = x(x + 2)$，$S_{左视图}=x^{2}+x = x(x + 1)$，
∴俯视图的长为$x + 2$，宽为$x + 1$，
∴$S_{俯视图}=(x + 2)(x + 1)=x^{2}+3x + 2$.
故选：D.

11. 如图是一个几何体的三视图，若这个几何体的体积是36，则它的表面积是________.

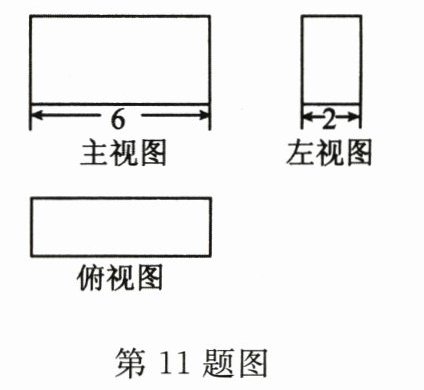
答案： 72 【解析】由三视图可知，此几何体为长方体，由主视图得出长方体的长是6，由左视图得出长方体的宽是2.
又这个几何体的体积是36，
∴长方体的高为：$36\div6\div2 = 3$，
∴长方体的表面积为：$2\times(3\times2 + 6\times2 + 3\times6)=72$.
故答案为：72.

12. 如图是一个几何体的三视图，其中主视图与左视图都是边长为4的等边三角形，则这个几何体的侧面展开图的面积为________.

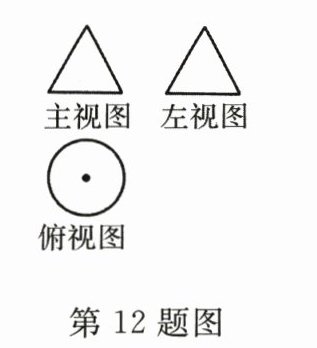
答案： $8\pi$ 【解析】由三视图可知这个几何体为圆锥，且圆锥的母线长为4，底面圆的直径为4，所以这个几何体的侧面展开图的面积为：$\frac{1}{2}\times4\pi\times4 = 8\pi$.
故答案为：$8\pi$.

13. 一个几何体的三视图如图所示，其中主视图和俯视图都是矩形，则它的表面积是________.

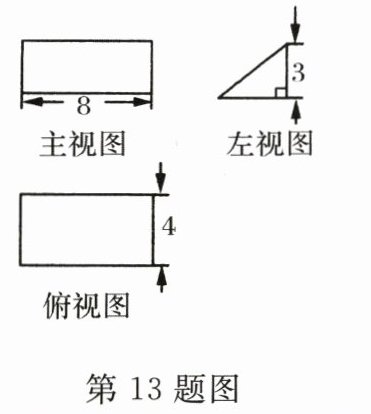
答案： 108 【解析】由三视图可判断出这个几何体为三棱柱，是由3个矩形和2个三角形组成，其中，三角形为直角三角形，两直角边分别为3，4，所以该几何体的表面积为：$(3 + 4 + 5)\times8+2\times\frac{1}{2}\times3\times4 = 108$.
故答案为：108.

14. 如图是某工件的三视图，求此工件的全面积和体积.

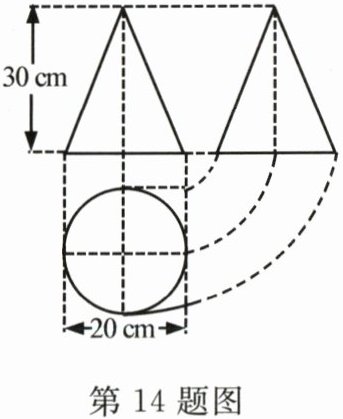
答案： 解：由三视图可知，该工件是底面半径为10 cm，高为30 cm的圆锥体.
∴母线长$l=\sqrt{30^{2}+10^{2}} = 10\sqrt{10}(cm)$，
∴$S_{侧}=\frac{1}{2}\times20\pi\times10\sqrt{10}=100\sqrt{10}\pi(cm^{2})$，
$S_{底}=10^{2}\pi = 100\pi(cm^{2})$，
∴$S_{全}=100\pi+100\sqrt{10}\pi = 100(1+\sqrt{10})\pi(cm^{2})$，
$V=\frac{1}{3}\times100\pi\times30 = 1000\pi(cm^{3})$.
答：此工件的全面积是$100(1+\sqrt{10})\pi cm^{2}$，体积是$1000\pi cm^{3}$.