第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
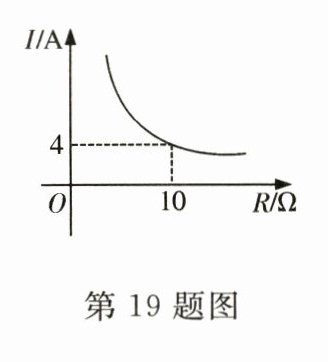
19.(跨学科)已知蓄电池的电压为定值.使用此蓄电池作为电源时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的表达式;
(2)如果以此蓄电池为电源的用电器的电流不能超过8A,那么该用电器的可变电阻至少是多少?
(1)求这个反比例函数的表达式;
(2)如果以此蓄电池为电源的用电器的电流不能超过8A,那么该用电器的可变电阻至少是多少?

答案:
19. 解:
(1)设反比例函数的表达式为$I = \frac{k}{R}$,
将点$(10,4)$代入得$4 = \frac{k}{10}$,解得$k = 40$,
∴这个反比例函数的表达式为$I = \frac{40}{R}$.
(2)由题可知,当$I = 8$时,$R = 5$,且$I$随着$R$的增大而减小,
∴当$I\leq 8$时,$R\geq 5$,
∴该用电器的可变电阻至少是 5 $\Omega$.
(1)设反比例函数的表达式为$I = \frac{k}{R}$,
将点$(10,4)$代入得$4 = \frac{k}{10}$,解得$k = 40$,
∴这个反比例函数的表达式为$I = \frac{40}{R}$.
(2)由题可知,当$I = 8$时,$R = 5$,且$I$随着$R$的增大而减小,
∴当$I\leq 8$时,$R\geq 5$,
∴该用电器的可变电阻至少是 5 $\Omega$.
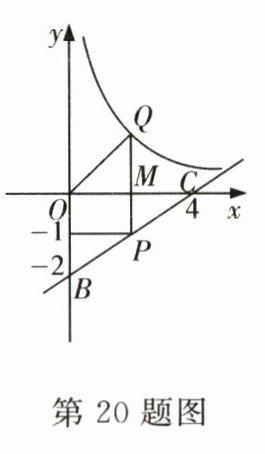
20.如图,经过点B(0,−2),C(4,0)的直线上有一点P(a,−1),过点P作PQ⊥x轴于M,交反比例函数y=$\frac{k}{x}$在第一象限的图象于点Q,连接OQ,S△oMQ=$\frac{3}{2}$.
(1)求直线BC的函数解析式;
(2)求Q点的坐标.
(1)求直线BC的函数解析式;
(2)求Q点的坐标.

答案:
20. 解:
(1)设直线$BC$的函数解析式为$y = kx + b$,
由题意,得$\begin{cases}b = -2\\4k + b = 0\end{cases}$,解得$\begin{cases}b = -2\\k = \frac{1}{2}\end{cases}$,
∴直线$BC$的函数解析式为$y = \frac{1}{2}x - 2$.
(2)令$y = -1$得,$\frac{1}{2}x - 2 = -1$,解得$x = 2$,
∴$P(2,-1)$.
∵$S_{\triangle OMQ} = \frac{3}{2}$,
∴$k = 3$,
∴反比例函数的解析式为$y = \frac{3}{x}$.
∵$PQ\perp x$轴,
∴点$Q$的横坐标为 2,
当$x = 2$时,$y = \frac{3}{2}$,
∴$Q(2,\frac{3}{2})$.
(1)设直线$BC$的函数解析式为$y = kx + b$,
由题意,得$\begin{cases}b = -2\\4k + b = 0\end{cases}$,解得$\begin{cases}b = -2\\k = \frac{1}{2}\end{cases}$,
∴直线$BC$的函数解析式为$y = \frac{1}{2}x - 2$.
(2)令$y = -1$得,$\frac{1}{2}x - 2 = -1$,解得$x = 2$,
∴$P(2,-1)$.
∵$S_{\triangle OMQ} = \frac{3}{2}$,
∴$k = 3$,
∴反比例函数的解析式为$y = \frac{3}{x}$.
∵$PQ\perp x$轴,
∴点$Q$的横坐标为 2,
当$x = 2$时,$y = \frac{3}{2}$,
∴$Q(2,\frac{3}{2})$.
21.已知反比例函数y=$\frac{m−3}{x}$(m为常数,且m≠3).
(1)若在其图象的每一个分支上,y随x增大而减小,求m的取值范围;
(2))若点A(2,$\frac{3}{2}$)在该反比例函数的图象上;
①求m的值;
②当x<−1时,请直接写出y的取值范围.
(1)若在其图象的每一个分支上,y随x增大而减小,求m的取值范围;
(2))若点A(2,$\frac{3}{2}$)在该反比例函数的图象上;
①求m的值;
②当x<−1时,请直接写出y的取值范围.
答案:
21. 解:
(1)由题意得,$m - 3>0$,解得$m>3$.
(2)①把$A(2,\frac{3}{2})$代入$y = \frac{m - 3}{x}$中,
得$m - 3 = 3$,解得$m = 6$.
②$-3<y<0$.
(1)由题意得,$m - 3>0$,解得$m>3$.
(2)①把$A(2,\frac{3}{2})$代入$y = \frac{m - 3}{x}$中,
得$m - 3 = 3$,解得$m = 6$.
②$-3<y<0$.
22.已知某品牌运动鞋每双进价为120元,为求合适的销售价格进行了4天的试销,试销情况如下表:
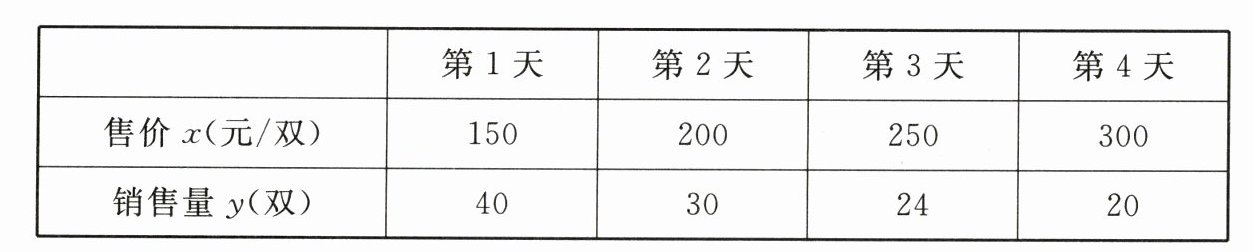
(1)表中数据x,y满足什么函数关系?请求出其函数关系式;
(2)若每天销售利润为3000元,则售价应定为多少元?

(1)表中数据x,y满足什么函数关系?请求出其函数关系式;
(2)若每天销售利润为3000元,则售价应定为多少元?
答案:
22. 解:
(1)由表中数据得:$xy = 6000$,
∴$y = \frac{6000}{x}$,
∴$y$是$x$的反比例函数,
$y$与$x$之间的函数关系式为$y = \frac{6000}{x}$.
(2)由题意,得$(x - 120)\cdot\frac{6000}{x} = 3000$,
解得$x = 240$.
经检验,$x = 240$是原方程的解,且符合题意.
答:若商场计划每天的销售利润为 3000 元,则其售价应定为 240 元.
(1)由表中数据得:$xy = 6000$,
∴$y = \frac{6000}{x}$,
∴$y$是$x$的反比例函数,
$y$与$x$之间的函数关系式为$y = \frac{6000}{x}$.
(2)由题意,得$(x - 120)\cdot\frac{6000}{x} = 3000$,
解得$x = 240$.
经检验,$x = 240$是原方程的解,且符合题意.
答:若商场计划每天的销售利润为 3000 元,则其售价应定为 240 元.
23.已知A,B两地相距480千米,小明驾车从A地出发,匀速驶往B地参加活动.
(1)设小明行驶的时间为x小时,行驶的速度为y千米/小时,则y关于x的函数表达式为________;
(2)若从A地到B地全程速度限定为不超过120千米/小时,小明早上8:00出发,则他到达B 地最早的时刻是________;
(3)活动结束后,小明按原路返回.返回的速度比他出发的速度每小时快10千米,返回到A地所需时间是他从A地到B地所需时间的$\frac{5}{6}$,求小明返回到A地所需的时间.
(1)设小明行驶的时间为x小时,行驶的速度为y千米/小时,则y关于x的函数表达式为________;
(2)若从A地到B地全程速度限定为不超过120千米/小时,小明早上8:00出发,则他到达B 地最早的时刻是________;
(3)活动结束后,小明按原路返回.返回的速度比他出发的速度每小时快10千米,返回到A地所需时间是他从A地到B地所需时间的$\frac{5}{6}$,求小明返回到A地所需的时间.
答案:
23. 解:
(1)$y = \frac{480}{x}$
(2)$12:00$
(3)设小明从$A$地到$B$地所用的时间为$t$小时,
根据题意,得$\frac{480}{t}+10 = \frac{480}{\frac{5}{6}t}$,解得$t = \frac{48}{5}$,
经检验:$t = \frac{48}{5}$是原分式方程的解,且符合实际,
当$t = \frac{48}{5}$时,$\frac{5}{6}t = 8$,
答:小明返回到$A$地所需时间为 8 小时.
(1)$y = \frac{480}{x}$
(2)$12:00$
(3)设小明从$A$地到$B$地所用的时间为$t$小时,
根据题意,得$\frac{480}{t}+10 = \frac{480}{\frac{5}{6}t}$,解得$t = \frac{48}{5}$,
经检验:$t = \frac{48}{5}$是原分式方程的解,且符合实际,
当$t = \frac{48}{5}$时,$\frac{5}{6}t = 8$,
答:小明返回到$A$地所需时间为 8 小时.
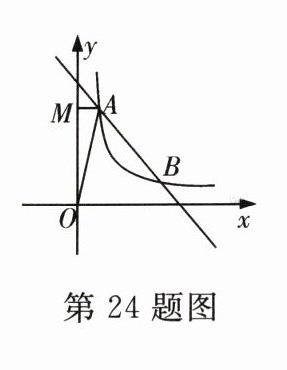
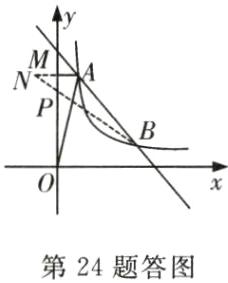
24.如图,在平面直角坐标系中,一次函数y=mx+5(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积;
(3)在y轴上求一点P,使PA+PB的值最小,并求出此时点P的坐标.
(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积;
(3)在y轴上求一点P,使PA+PB的值最小,并求出此时点P的坐标.

答案:
24. 解:
(1)将$B(4,1)$代入$y = \frac{k}{x}$,得
$\frac{k}{4} = 1$,解得$k = 4$,
∴反比例函数的解析式为$y = \frac{4}{x}$.
将$B(4,1)$代入$y = mx + 5$,得
$1 = 4m + 5$,解得$m = -1$.
∴一次函数的解析式为$y = -x + 5$.
(2)将$A(1,n)$代入$y = \frac{4}{x}$中,得$n = 4$,
∴点$A$的坐标为$(1,4)$,
∴$S_{\triangle OAM} = \frac{1}{2}\times 1\times 4 = 2$.
(3)如图,作点$A$关于$y$轴的对称点$N$,
则$N(-1,4)$.
连接$BN$,交$y$轴于点$P$,点$P$即为所求.
设直线$BN$的解析式为$y = k_1x + b$,
将$B(4,1)$,$N(-1,4)$代入,得
$\begin{cases}4k_1 + b = 1\\-k_1 + b = 4\end{cases}$,解得$\begin{cases}k_1 = -\frac{3}{5}\\b = \frac{17}{5}\end{cases}$,
∴直线$BN$的解析式为$y = -\frac{3}{5}x + \frac{17}{5}$,
当$x = 0$时,$y = \frac{17}{5}$,
∴点$P$的坐标为$(0,\frac{17}{5})$.
24. 解:
(1)将$B(4,1)$代入$y = \frac{k}{x}$,得
$\frac{k}{4} = 1$,解得$k = 4$,
∴反比例函数的解析式为$y = \frac{4}{x}$.
将$B(4,1)$代入$y = mx + 5$,得
$1 = 4m + 5$,解得$m = -1$.
∴一次函数的解析式为$y = -x + 5$.
(2)将$A(1,n)$代入$y = \frac{4}{x}$中,得$n = 4$,
∴点$A$的坐标为$(1,4)$,
∴$S_{\triangle OAM} = \frac{1}{2}\times 1\times 4 = 2$.
(3)如图,作点$A$关于$y$轴的对称点$N$,
则$N(-1,4)$.
连接$BN$,交$y$轴于点$P$,点$P$即为所求.

设直线$BN$的解析式为$y = k_1x + b$,
将$B(4,1)$,$N(-1,4)$代入,得
$\begin{cases}4k_1 + b = 1\\-k_1 + b = 4\end{cases}$,解得$\begin{cases}k_1 = -\frac{3}{5}\\b = \frac{17}{5}\end{cases}$,
∴直线$BN$的解析式为$y = -\frac{3}{5}x + \frac{17}{5}$,
当$x = 0$时,$y = \frac{17}{5}$,
∴点$P$的坐标为$(0,\frac{17}{5})$.
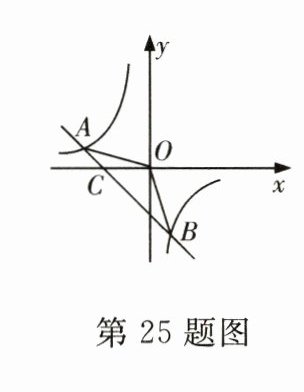
25.如图,一次函数y=kx十b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(−2,1),B(1,n),与x 轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)根据所给条件,请直接写出不等式kx十b<$\frac{m}{x}$的解集.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)根据所给条件,请直接写出不等式kx十b<$\frac{m}{x}$的解集.

答案:
25. 解:
(1)把点$A(-2,1)$代入$y = \frac{m}{x}$,得
$1 = \frac{m}{-2}$,解得$m = -2$,
即反比例函数的解析式为$y = -\frac{2}{x}$,
当$x = 1$时,$n = -2$,
∴点$B$的坐标为$(1,-2)$.
把$A(-2,1)$,$B(1,-2)$分别代入$y = kx + b$,得
$\begin{cases}-2k + b = 1\\k + b = -2\end{cases}$,解得$\begin{cases}k = -1\\b = -1\end{cases}$,
∴一次函数的解析式为$y = -x - 1$.
(2)令$y = 0$得,$-x - 1 = 0$,解得$x = -1$,
∴点$C$的坐标为$(-1,0)$,
∴$OC = 1$,
∴$S_{\triangle AOB} = \frac{1}{2}\times 1\times 1 + \frac{1}{2}\times 1\times 2 = \frac{3}{2}$.
(3)$-2<x<0$或$x>1$.
(1)把点$A(-2,1)$代入$y = \frac{m}{x}$,得
$1 = \frac{m}{-2}$,解得$m = -2$,
即反比例函数的解析式为$y = -\frac{2}{x}$,
当$x = 1$时,$n = -2$,
∴点$B$的坐标为$(1,-2)$.
把$A(-2,1)$,$B(1,-2)$分别代入$y = kx + b$,得
$\begin{cases}-2k + b = 1\\k + b = -2\end{cases}$,解得$\begin{cases}k = -1\\b = -1\end{cases}$,
∴一次函数的解析式为$y = -x - 1$.
(2)令$y = 0$得,$-x - 1 = 0$,解得$x = -1$,
∴点$C$的坐标为$(-1,0)$,
∴$OC = 1$,
∴$S_{\triangle AOB} = \frac{1}{2}\times 1\times 1 + \frac{1}{2}\times 1\times 2 = \frac{3}{2}$.
(3)$-2<x<0$或$x>1$.
26.如图,已知点A(m,2)是直线l与双曲线y=$\frac{3}{x}$的交点.
(1)求m的值;
(2)若直线L分别和x轴、y轴交于E,F两点,且点A是EF的中点,试确定直线L的解析式;
(3)在双曲线y=$\frac{3}{x}$上另取一点B,过点B作BK⊥x轴于K,试问:在y轴上是否存在点P,使得S△PAF=S△BOK?若存在,请求出点P的坐标;若不存在,请说明理由.
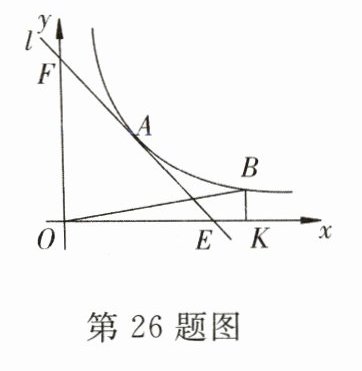
(1)求m的值;
(2)若直线L分别和x轴、y轴交于E,F两点,且点A是EF的中点,试确定直线L的解析式;
(3)在双曲线y=$\frac{3}{x}$上另取一点B,过点B作BK⊥x轴于K,试问:在y轴上是否存在点P,使得S△PAF=S△BOK?若存在,请求出点P的坐标;若不存在,请说明理由.

答案:
26. 解:
(1)把$A(m,2)$代入$y = \frac{3}{x}$,得
$2 = \frac{3}{m}$,解得$m = \frac{3}{2}$.
(2)
∵点$A(\frac{3}{2},2)$是$EF$的中点,
∴点$E$的坐标为$(3,0)$,点$F$的坐标为$(0,4)$.
设直线$l$的解析式为$y = kx + b$,
把$E(3,0)$,$F(0,4)$代入,得
$\begin{cases}3k + b = 0\\b = 4\end{cases}$,解得$\begin{cases}k = -\frac{4}{3}\\b = 4\end{cases}$,
∴直线$l$的解析式为$y = -\frac{4}{3}x + 4$.
(3)存在.
设点$P$的坐标为$(0,t)$,则$PF = |4 - t|$.
∵$S_{\triangle PAF} = S_{\triangle EOK} = \frac{1}{2}\times 3 = \frac{3}{2}$,
∴$\frac{1}{2}\times |4 - t|\times\frac{3}{2} = \frac{3}{2}$,
解得$t = 6$或 2,
∴满足条件的点$P$的坐标为$(0,6)$或$(0,2)$.
(1)把$A(m,2)$代入$y = \frac{3}{x}$,得
$2 = \frac{3}{m}$,解得$m = \frac{3}{2}$.
(2)
∵点$A(\frac{3}{2},2)$是$EF$的中点,
∴点$E$的坐标为$(3,0)$,点$F$的坐标为$(0,4)$.
设直线$l$的解析式为$y = kx + b$,
把$E(3,0)$,$F(0,4)$代入,得
$\begin{cases}3k + b = 0\\b = 4\end{cases}$,解得$\begin{cases}k = -\frac{4}{3}\\b = 4\end{cases}$,
∴直线$l$的解析式为$y = -\frac{4}{3}x + 4$.
(3)存在.
设点$P$的坐标为$(0,t)$,则$PF = |4 - t|$.
∵$S_{\triangle PAF} = S_{\triangle EOK} = \frac{1}{2}\times 3 = \frac{3}{2}$,
∴$\frac{1}{2}\times |4 - t|\times\frac{3}{2} = \frac{3}{2}$,
解得$t = 6$或 2,
∴满足条件的点$P$的坐标为$(0,6)$或$(0,2)$.
1.下列图形中,不是相似图形的一组是 ( )
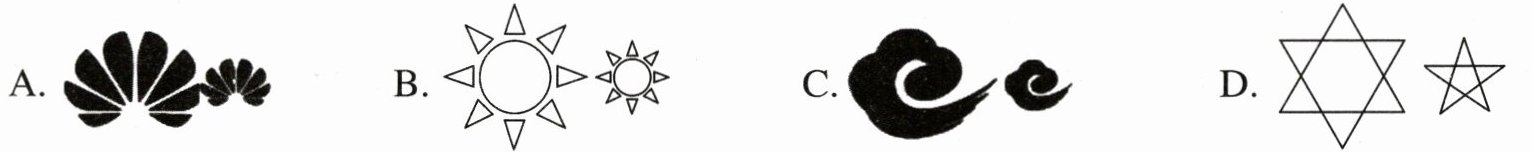
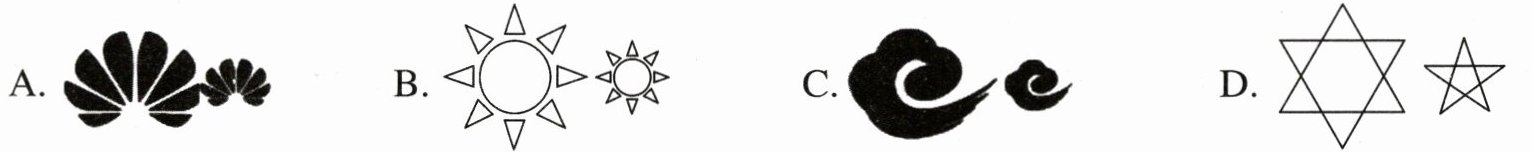
答案:
D
2.在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为 ( )
A.125km
B.12.5km
C.1.25km
D.1250km
A.125km
B.12.5km
C.1.25km
D.1250km
答案:
A [解析]设实际距离为$x\ cm$,
则$1:500000 = 25:x$,解得$x = 12500000$。
$12500000\ cm = 125\ km$。故选:A。
则$1:500000 = 25:x$,解得$x = 12500000$。
$12500000\ cm = 125\ km$。故选:A。
3.如图,四边形ABCD和四边形EFGH相似,且顶点都在方格纸的格点上,则四边形ABCD与四边形EFGH的相似比是 ( )
A.1:2 B.1:4 C.2:1 D.4:1
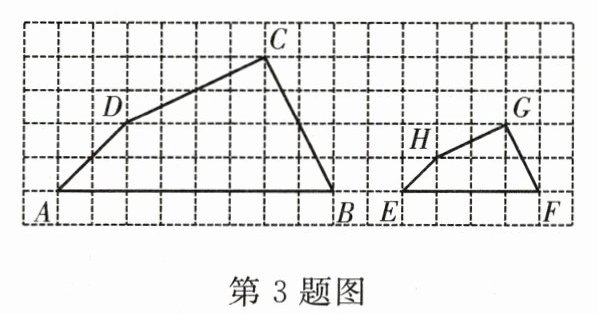
A.1:2 B.1:4 C.2:1 D.4:1

答案:
C
4.【易错题】下列各组线段中,成比例的是 ( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
答案:
D [解析]A. $\because2\times5\neq3\times4$,$\therefore$选项A不成比例;
B. $\because2\times8\neq4\times6$,$\therefore$选项B不成比例;
C. $\because3\times12\neq6\times8$,$\therefore$选项C不成比例;
D. $\because1\times15 = 3\times5$,$\therefore$选项D成比例。故选:D。
B. $\because2\times8\neq4\times6$,$\therefore$选项B不成比例;
C. $\because3\times12\neq6\times8$,$\therefore$选项C不成比例;
D. $\because1\times15 = 3\times5$,$\therefore$选项D成比例。故选:D。
5.如图,四边形ABCD与四边形EFGH相似,∠A=80°,∠C=90°,∠F=70°,则∠H等于( )
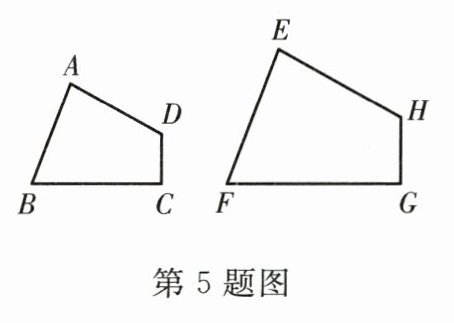
A.70°
B.80°
C.110°
D.120°

A.70°
B.80°
C.110°
D.120°
答案:
D [解析]$\because$四边形$ABCD$与四边形$EFGH$相似,$\angle A = 80^{\circ}$,$\angle C = 90^{\circ}$,$\angle F = 70^{\circ}$,
$\therefore\angle E=\angle A = 80^{\circ}$,$\angle G=\angle C = 90^{\circ}$,
$\therefore\angle H = 360^{\circ}-\angle E-\angle F-\angle G = 360^{\circ}-80^{\circ}-70^{\circ}-90^{\circ}=120^{\circ}$。
故选:D。
$\therefore\angle E=\angle A = 80^{\circ}$,$\angle G=\angle C = 90^{\circ}$,
$\therefore\angle H = 360^{\circ}-\angle E-\angle F-\angle G = 360^{\circ}-80^{\circ}-70^{\circ}-90^{\circ}=120^{\circ}$。
故选:D。
6.如图,有甲,乙、丙三个矩形,下列说法正确的是 ( )
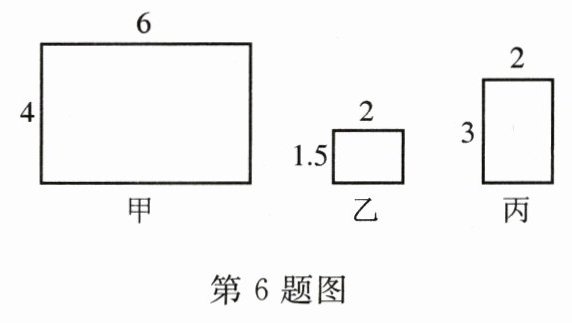
A.甲与丙相似
B.甲与乙相似
C.乙与丙相似
D.三个矩形都不相似

A.甲与丙相似
B.甲与乙相似
C.乙与丙相似
D.三个矩形都不相似
答案:
A [解析]三个矩形的角都是直角,甲、乙、丙三个矩形相邻两边的比分别为$2:3$,$3:4$,$2:3$,所以甲与丙相似。
故选:A。
故选:A。
7.一个零件的高是5mm,画在图纸上的高是2cm,这幅图的比例尺是__________.
答案:
$4:1$ [解析]$2\ cm = 20\ mm$,
这幅图的比例尺为$20\ mm:5\ mm = 4:1$。
故答案为:$4:1$。
这幅图的比例尺为$20\ mm:5\ mm = 4:1$。
故答案为:$4:1$。
8.若$\frac{a}{2}=\frac{b}{3}$,则$\frac{a}{a + b}$的值为__________.
答案:
$\frac{2}{5}$ [解析]$\because\frac{a}{2}=\frac{b}{3}$,$\therefore b=\frac{3}{2}a$,
$\therefore\frac{a}{a + b}=\frac{a}{a+\frac{3}{2}a}=\frac{2}{5}$。
故答案为:$\frac{2}{5}$。
$\therefore\frac{a}{a + b}=\frac{a}{a+\frac{3}{2}a}=\frac{2}{5}$。
故答案为:$\frac{2}{5}$。
9.已知两个相似的五边形,其中一个各边长分别为1,2,3,4,5,若另一个最长边为10,则这个五边形的最短边长为__________.
答案:
$2$ [解析]设这个五边形的最短边长为$x$,
则$1:x = 5:10$,解得$x = 2$,
故答案为:$2$。
则$1:x = 5:10$,解得$x = 2$,
故答案为:$2$。
查看更多完整答案,请扫码查看


