《2025年名校调研跟踪测试卷九年级数学下册人教版》

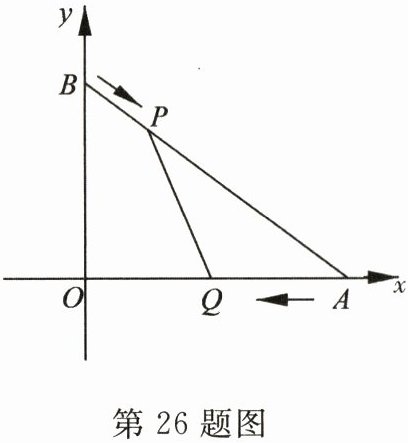
26. 如图，在平面直角坐标系中，已知点$A(4,0)$，点$B(0,3)$，点$P$从点$B$出发沿$BA$方向向点$A$匀速运动，速度为每秒1个单位长度，点$Q$从点$A$出发沿$AO$方向向点$O$匀速运动，速度为每秒2个单位长度，连接$PQ$. 设运动的时间为$t$秒$(0＜t＜2)$.
(1)求直线$AB$的解析式；
(2)设$\triangle AQP$的面积为$y$，求$y$与$t$之间的函数关系式；
(3)是否存在某一时刻$t$，使线段$PQ$恰好把$\triangle AOB$的周长和面积同时平分？若存在，请求出此时$t$的值；若不存在，请说明理由；
(4)连接$PO$，并把$\triangle PQO$沿$QO$翻折，得到四边形$POP'Q$，那么是否存在某一时刻$t$，使四边形$POP'Q$为菱形？若存在，请求出此时点$Q$的坐标和菱形的边长；若不存在，请说明理由.
　　

答案： 解：
(1)设直线$AB$的解析式为$y = kx + b$，将点$A(4,0)$，$B(0,3)$代入得，$\begin{cases}4k + b = 0\\b = 3\end{cases}$，解得$\begin{cases}k = -\frac{3}{4}\\b = 3\end{cases}$，$\therefore$直线$AB$的解析式是$y = -\frac{3}{4}x + 3$.
(2)在$Rt\triangle AOB$中，$AB=\sqrt{BO^{2}+AO^{2}} = 5$. 依题意，得$BP = t$，$AP = 5 - t$，$AQ = 2t$. 过点$P$作$PM\perp AO$于点$M$，则$PM// BO$，$\therefore\triangle APM\sim\triangle ABO$，$\therefore\frac{PM}{BO}=\frac{AP}{AB}$，即$\frac{PM}{3}=\frac{5 - t}{5}$，$\therefore PM = 3-\frac{3}{5}t$，$\therefore y=\frac{1}{2}AQ\cdot PM=\frac{1}{2}×2t(3-\frac{3}{5}t)=-\frac{3}{5}t^{2}+3t$.
(3)不存在. 理由如下：当$PQ$平分$\triangle AOB$的周长时，$AP + AQ = 6$，即$(5 - t)+2t = 6$，解得$t = 1$. 当$PQ$平分$\triangle AOB$的面积时，$S_{\triangle APQ}=\frac{1}{2}S_{\triangle AOB}$，即$-\frac{3}{5}t^{2}+3t = 3$. 当$t = 1$时，$-\frac{3}{5}×1+3×1=\frac{12}{5}\neq3$，$\therefore$不存在某一时刻$t$，使线段$PQ$把$\triangle AOB$的周长和面积同时平分.
(4)存在某一时刻$t$，使四边形$POP'Q$为菱形. 过点$P$作$PN\perp BO$于$N$，若四边形$POP'Q$是菱形，则有$PQ = PO$. $\because PM\perp AO$于$M$，$\therefore QM = OM$. $\because PN// OA$，$\therefore\triangle PBN\sim\triangle ABO$，$\therefore\frac{PN}{AO}=\frac{PB}{AB}$，即$\frac{PN}{4}=\frac{t}{5}$，$\therefore PN=\frac{4}{5}t$，$\therefore QM = OM=\frac{4}{5}t$，$\therefore\frac{4}{5}t+\frac{4}{5}t+2t = 4$，解得$t=\frac{10}{9}$，$\therefore$当$t=\frac{10}{9}$时，四边形$POP'Q$是菱形，$\therefore OM=\frac{4}{5}t=\frac{8}{9}$，$PM = 3-\frac{3}{5}t=\frac{7}{3}$，$\therefore OQ = 2OM=\frac{16}{9}$，$\therefore$点$Q$的坐标为$(\frac{16}{9},0)$. 在$Rt\triangle PMO$中，$OP=\sqrt{PM^{2}+OM^{2}}=\sqrt{(\frac{7}{3})^{2}+(\frac{8}{9})^{2}}=\frac{\sqrt{505}}{9}$，即菱形$POP'Q$的边长为$\frac{\sqrt{505}}{9}$.