《2025年名校调研跟踪测试卷九年级数学下册人教版》

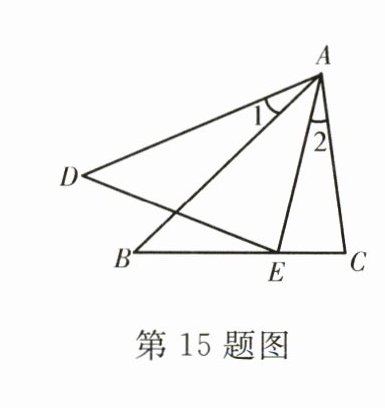
15. 如图，$AB\cdot AE = AD\cdot AC$，且$\angle 1 = \angle 2$，求证：$\triangle ABC\sim\triangle ADE$.
　　
　

答案： 证明：$\because AB\cdot AE = AD\cdot AC$，$\therefore\frac{AB}{AD}=\frac{AC}{AE}$. 又$\because\angle 1=\angle 2$，$\therefore\angle 2+\angle BAE=\angle 1+\angle BAE$，即$\angle BAC=\angle DAE$，$\therefore\triangle ABC\sim\triangle ADE$.

16. 反比例函数$y = \frac{k}{x}(k\neq0)$的图象经过点$(-5,-2)$，若点$(n,1)$也在此反比例函数的图象上，求$n$的值.

答案： $n = 10$.

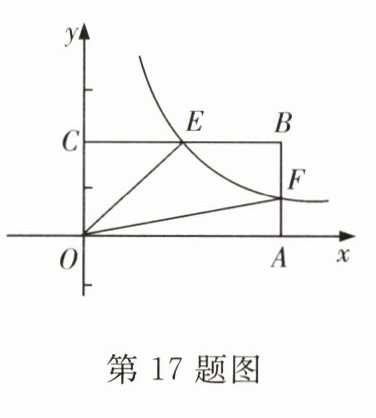
17. 如图，双曲线$y = \frac{k}{x}$经过矩形$ABCD$边$AB$的中点$F(4,1)$，交$BC$边于点$E$.
(1)求双曲线的函数解析式；
(2)求四边形$OEBF$的面积.
　　　

答案： 解：
(1)将点$F(4,1)$代入$y=\frac{k}{x}$得，$k = 4$，$\therefore$双曲线的函数解析式为$y=\frac{4}{x}$.
(2)$\because F(4,1)$为边$AB$的中点，$\therefore B(4,2)$，$\therefore S_{矩形 OABC}=4×2 = 8$，$S_{\triangle OEC}=S_{\triangle OAF}=2$，$\therefore S_{四边形 OEBF}=S_{四边形 OABC}-S_{\triangle OEC}-S_{\triangle OAF}=8 - 2 - 2 = 4$.

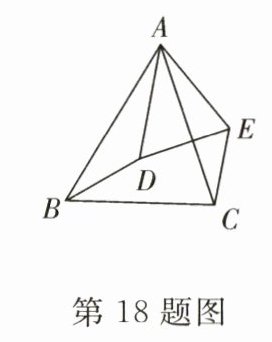
18. 如图，已知$\triangle ABD\sim\triangle ACE$，$\angle ABC = 50^{\circ}$，$\angle BAC = 60^{\circ}$，求$\angle AED$的度数.
　

答案： 解：$\because\angle ABC = 50^{\circ}$，$\angle BAC = 60^{\circ}$，$\therefore\angle ACB = 180^{\circ}-\angle ABC-\angle BAC = 70^{\circ}$. $\because\triangle ABD\sim\triangle ACE$，$\therefore\frac{AB}{AC}=\frac{AD}{AE}$，$\angle BAD=\angle CAE$，$\therefore\frac{AB}{AD}=\frac{AC}{AE}$，$\angle BAC=\angle DAE$，$\therefore\triangle BAC\sim\triangle DAE$，$\therefore\angle AED=\angle ACB = 70^{\circ}$.

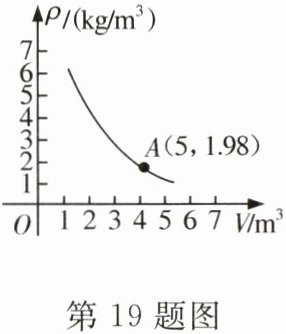
19. 跨学科 密闭容器内有一定质量的二氧化碳，当容器的体积$V$(单位：$m^3$)变化时，气体的密度$\rho$(单位：$kg/m^3$)随之变化，已知密度$\rho$与体积$V$是反比例函数关系，它的图象如图所示.
(1)求密度$\rho$关于体积$V$的函数解析式；
(2)当$V = 9$ $m^3$时，求二氧化碳的密度$\rho$.
　　　

答案： 解：
(1)设$\rho$关于$V$的函数解析式为$\rho=\frac{k}{V}$，将点$(5,1.98)$代入，得$k = 9.9$，$\therefore\rho$关于$V$的函数解析式为$\rho=\frac{9.9}{V}(V\gt0)$.
(2)当$V = 9$时，$\rho=\frac{9.9}{9}=1.1(kg/m^{3})$.

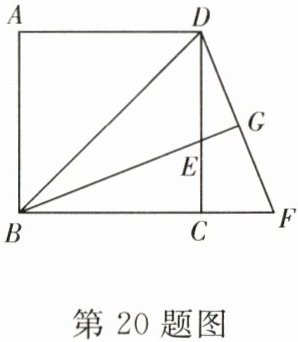
20. 如图，在正方形$ABCD$中，$BE$平分$\angle DBC$且交$CD$于点$E$，将$\triangle BCE$绕点$C$顺时针旋转到$\triangle DCF$的位置，并延长$BE$交$DF$于点$G$. 求证：
(1)$\triangle BDG\sim\triangle DEG$；
(2)$BG\perp DF$.
　　　

答案： 证明：
(1)由旋转可知，$\angle FDC=\angle EBC$. $\because BE$平分$\angle DBC$，$\therefore\angle DBE=\angle EBC$，$\therefore\angle FDC=\angle DBE$. 又$\angle DGE=\angle DGB$，$\therefore\triangle BDG\sim\triangle DEG$.
(2)$\because\angle EBC=\angle GDE$，$\angle BEC=\angle DEG$，$\therefore\angle DGE=\angle BCE = 90^{\circ}$，$\therefore BG\perp DF$.