《2025年名校调研跟踪测试卷九年级数学下册人教版》

21. 如图,一次函数$y = kx + b$的图象与反比例函数$y = \frac{m}{x}$的图象相交于$A(1,3),B(-3,n)$两点.
(1)求反比例函数与一次函数的解析式;
(2)在$x$轴上找一点$P$,使$\vert PA - PB\vert$的值最大,求满足条件的点$P$的坐标及$\triangle PAB$的面积.

答案：
解：
(1)将点A(1，3)代入$y = \frac{m}{x}$得m = 1×3 = 3，
∴反比例函数的解析式为$y = \frac{3}{x}$.
将B(－3，n)代入$y = \frac{3}{x}$，得n = $\frac{3}{-3}=-1$，
∴点B的坐标为(－3，－1).
将点A(1，3)，B(－3，－1)代入y = kx + b，得
$\begin{cases}-1=-3k + b\\3=k + b\end{cases}$，解得$\begin{cases}k = 1\\b = 2\end{cases}$，
∴一次函数的表达式为y = x + 2.
(2)如图，过点A作x轴的对称点A′(1，－3)，连接A′B并延长交x轴于点P，则|PA－PB| = |PA′－PB| = A′B为最大.
由点A′，B的坐标可得直线A′P的表达式为
$y = -\frac{1}{2}x-\frac{5}{2}$，
令y = 0，得x = －5，故点P的坐标为(－5，0)，
∴$S_{\triangle PAB}=S_{\triangle AA'P}-S_{\triangle AA'B}=\frac{1}{2}×(3 + 3)×(5 - 3)=6$.

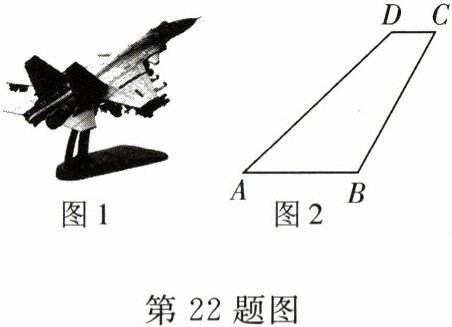
22. 随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据,$BC = 8,CD = 2,\angle D = 135^{\circ},\angle C = 60^{\circ}$,且$AB// CD$,求出垂尾模型$ABCD$的面积.(结果保留整数.参考数据:$\sqrt{2}\approx1.414,\sqrt{3}\approx1.732$)

答案：
解：如图，过点A作CD的垂线，交CD的延长线于点F，过点C作AB的垂线，交AB的延长线于点E.

∵AB//CD，
∴四边形AECF是矩形.
∵∠BCD = 60°，
∴∠BCE = 90°－60° = 30°，
∴BE = $\frac{1}{2}BC = 4$，CE = $\frac{\sqrt{3}}{2}BC = 4\sqrt{3}$.
∵∠ADC = 135°，
∴∠ADF = 180°－135° = 45°，
∴△ADF是等腰直角三角形，
∴DF = AF = CE = 4\sqrt{3}$.∵FC = AE，即4\sqrt{3}+2 = AB + 4，∴AB = 4\sqrt{3}-2，∴$S_{梯形ABCD}=\frac{1}{2}×(2 + 4\sqrt{3}-2)×4\sqrt{3}=24$.
答：垂尾模型ABCD的面积为24.