《2025年名校调研跟踪测试卷九年级数学下册人教版》

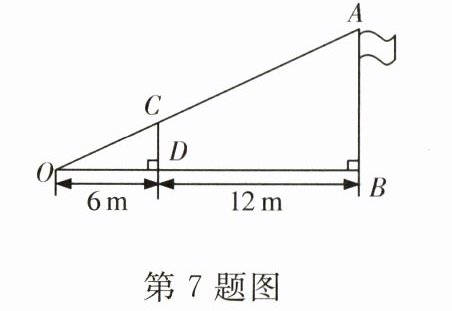
7.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度，移动竹竿,使竹竿顶端C、旗杆顶端A与O点在一条直线上,则根据图中数据可得旗杆AB的高为__________m.

答案： 9　[解析]由题意得，CD//AB，
　
∴△OCD∽△OAB,
　
∴$\frac{CD}{B}$=$\frac{OD}{OB}$,即$\frac{3}{AB}$=$\frac{6}{6+12}$,解得AB=9(m).
　　故答案为:9.

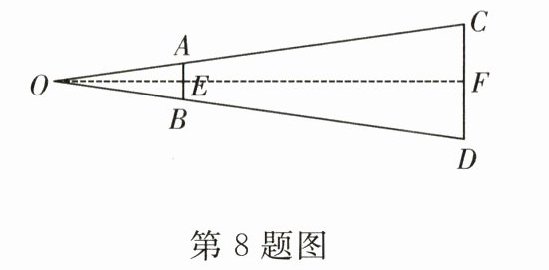
8.如图是步枪在瞄准时的示意图,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,若从眼睛到准星的距离OE为0.5m,则眼睛到目标的距离OF为__________m.

答案： 125　[解析]设眼睛到目标的距离为xm.
　　由题知,OE=0.5m,AB=0.2cm=0.002m,
CD=50cm=0.5m.
　
∵AB//CD,
∴△OAB∽△OCD,
　
∴$\frac{AB}{CD}$=$\frac{OE}{OF}$,即$\frac{0.002}{0.5}$=$\frac{0.5}{x}$,解得x=125(m).
　　故答案为:125.

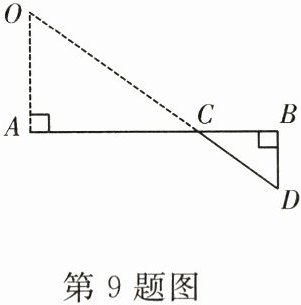
9.(真实情境)如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O,再在他们所在的这一侧选点A,B,D,使AB⊥AO,DB⊥AB,然后确定DO 和AB的交点C,测得AC =120m,CB =60m,BD =50m,请你帮助他们算出峡谷的宽AO.

答案： 解:
∵AB⊥AO,DB⊥AB,
∴∠A=∠B=90°,
　　又∠ACO=∠BCD,
　
∴△ACO∽△BCD,
∴$\frac{AO}{BD}$=$\frac{AC}{BC}$,
　　即$\frac{AO}{50}$=$\frac{120}{60}$,解得A0=100(m).
　　答:峡谷的宽A0是100m.

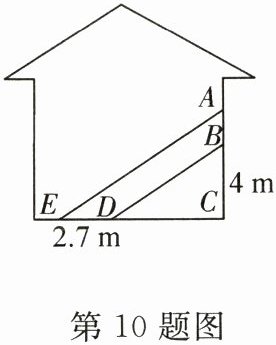
10.(真实情境)如图,阳光通过窗口AB照入到室内，在地面上形成一个宽2.7m的光亮区域DE,若光亮区域边缘E处到窗口所在墙的距离EC =8.7m,窗口底部到地面的高度BC =4m,求窗口AB的高度.

答案： 解:由题知,DC=EC−ED=6m.
　
∵太阳光是平行光线，
∴AE//BD,
　
∴△ECA∽△DCB,
　
∴$\frac{BC}{C}$=$\frac{DC}{EC}$，即$\frac{4}{AC}$=$\frac{6}{8.7}$,
　
∴AC=$\frac{4×8.7}{6}$=5.8(m),
　
∴AB=AC−BC=5.8−4=1.8(m).
　　　答:窗口AB的高度为1.8m.

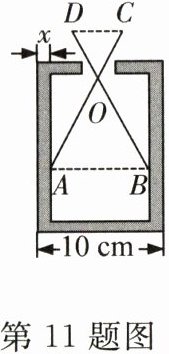
11.(十堰中考)如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC = OB:OD = 3,且量得CD = 3cm,则零件的厚度x为(　　)

A.0.3cm　　　　　　
　B.0.5cm　　　　　　　
　C.0.7cm　　　　　　　
　D.1cm

答案： B　[解析]
∵OA:OC=OB:OD=3,∠COD =∠AOB,
　
∴△COD∽△AOB,
∴AB:CD=3.
　
∵CD=3cm,
∴AB=9cm.
　
∵零件的外径为10cm，
　
∴零件的厚度x为:(10−9)÷2=0.5(cm).
　　　故选:B.