《2025年名校调研跟踪测试卷九年级数学下册人教版》

7. 计算:$\frac{1}{2}\sin60^{\circ}=$_______.

答案： $\frac{\sqrt{3}}{4}$

8. 任意写出一个经过第二、四象限的反比例函数的解析式:_______.

答案： $y = -\frac{3}{x}$(答案不唯一)

9. 已知$\triangle ABC$与$\triangle DEF$相似,且面积比为$9:25$,则$\triangle ABC$与$\triangle DEF$的相似比为_______.

答案： 3∶5

10. 若一次函数$y = ax + b(a,b$为常数)的图象经过第一、三、四象限,则函数$y = \frac{ab}{x}(a,b$为常数)的图象位于第_______象限.

答案： 二、四

11. 在锐角$\triangle ABC$中,若$\vert\sin A - \frac{\sqrt{3}}{2}\vert + (\cos B - \frac{\sqrt{2}}{2})^2 = 0$,则$\angle C$的度数是_______度.

答案： 75

12. 如图,$B,C$分别是反比例函数$y = \frac{6}{x}(x＞0)$与$y = -\frac{2}{x}(x＞0)$的图象上的点,且$BC// y$轴,过点$C$作$BC$的垂线交$y$轴于点$A$,则$\triangle ABC$的面积为_______.

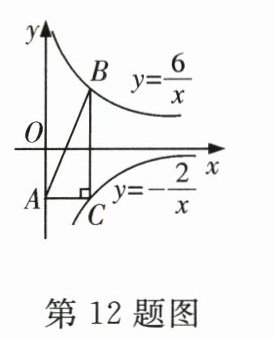
答案： 4

13. 如图,在平面直角坐标系中,$\triangle ABC$与$\triangle A_1B_1C_1$是位似图形,坐标原点$O$为位似中心.$A$与$A_1,B$与$B_1$是对应顶点.已知$A(-6,2),A_1(3,-1),BC = 5$,则$B_1C_1$的长为_______.

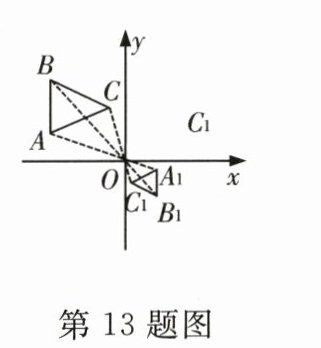
答案： $\frac{5}{2}$ [解析]
∵△ABC与△A₁B₁C₁是位似图形，坐标原点O为位似中心，A(－6,2)，A₁(3，－1)，
∴△A₁B₁C₁与△ABC的相似比为$\frac{1}{2}$，
∵BC = 5，$\frac{B_{1}C_{1}}{BC}=\frac{1}{2}$，
∴B₁C₁ = 5×$\frac{1}{2}=\frac{5}{2}$.
故答案为:$\frac{5}{2}$.

14. 如图,在$\square ABCD$中,$E,F$分别是边$AD,BC$的中点,$AC$分别交$BE,DF$于点$M,N$,给出下列结论:①$\triangle ABM\cong\triangle CDN$;②$AM = \frac{1}{3}AC$;③$DN = 2NF$;④$S_{\triangle AMB}=\frac{1}{2}S_{\triangle ABC}$,其中正确的结论是_______.(填序号)

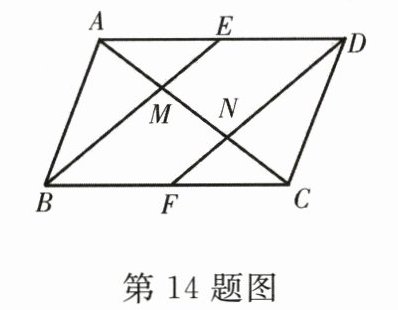
答案： ①②③ [解析]
∵四边形ABCD是平行四边形，
∴AB = CD，AD = BC，AD//BC，AB//CD.
∵AB//CD，
∴∠BAM = ∠DCN.
∵E，F分别是边AD，BC的中点，
∴AE = DE = $\frac{1}{2}AD$，CF = BF = $\frac{1}{2}BC$，
∴AE = ED = CF = BF.
又
∵DE//BF，
∴四边形DEBF为平行四边形，
∴BE//DF，
∴∠AMB = ∠MNF = ∠DNC.
∴△ABM≌△CDN. 故①正确；
∵AE//BC，
∴$\frac{AE}{BC}=\frac{AM}{MC}=\frac{1}{2}$，
∴2AM = MC，
∴AM = $\frac{1}{3}AC$. 故②正确；
同理可证得，DN = 2NF. 故③正确；
∵AM = $\frac{1}{3}AC$，
∴$S_{\triangle AMB}=\frac{1}{3}S_{\triangle ABC}$. 故④不正确.
故答案为:①②③.

15. 先化简,再求值:$(\frac{2}{a + 1} + \frac{a + 2}{a^2 - 1})\div\frac{a}{a - 1}$,其中$a = \tan60^{\circ}-2\sin30^{\circ}$.

答案： 解：原式 = $\frac{3}{a + 1}$.
当a = tan60°－2sin30° = $\sqrt{3}-1$时，
原式 = $\frac{3}{\sqrt{3}-1 + 1}=\sqrt{3}$.