《2025年名校调研跟踪测试卷九年级数学下册人教版》

7. 在一张比例尺是$50:1$的图纸上量得一昆虫的身长是$40$cm，则这只昆虫实际的身长是________cm.

答案： $0.8$

8. 如图，线段$AB$两个端点的坐标分别为$A(6,6)$，$B(9,3)$以原点$O$为位似中心，在第一象限内将线段$AB$缩小为原来的$\frac{1}{3}$后得到线段$CD$，则端点$D$的坐标为________.
　　　　　　

答案： $(3,1)$

9. 反比例函数$y = \frac{m + 1}{x}$的图象上有点$A(x_1,y_1)$，$B(x_2,y_2)$，且当$x_1＜x_2＜0$时，$y_1＜y_2$，则$m$的取值范围是________.

答案： $m\lt -1$

10. 真实情境 一把剪刀如图所示，$AB = 2BC$，$BD = 2BE$，当手握的地方$EC$张开$3$cm时，剪刀的尖端$A$，$D$两点的距离为________cm.

答案： $6$

11. 如图，在平面直角坐标系中，$\square OABC$的顶点$A$在反比例函数$y = \frac{1}{x}$上，顶点$B$在反比例函数$y = \frac{4}{x}$上，点$C$在$x$轴的正半轴上，则$\square OABC$的面积为________.

答案：
3【解析】如图，过点$A$，$B$分别作$x$轴的垂线，垂足分别为$M$，$N$，连接$BO$.

$\because$四边形$ABCO$是平行四边形，$\therefore OA = BC$，$AB// OC$，$\therefore AM = BN$，$\therefore Rt\triangle AOM\cong Rt\triangle BCN$，$\therefore S_{\triangle AOM}=S_{\triangle BCN}=\frac{1}{2}×1=\frac{1}{2}$. $\because S_{\triangle BON}=\frac{1}{2}×4 = 2$，$\therefore S_{\triangle OBC}=S_{\triangle BON}-S_{\triangle BCN}=2-\frac{1}{2}=\frac{3}{2}$，$\therefore S_{平行四边形 ABCO}=2S_{\triangle OBC}=3$. 故答案为：$3$.

12. 如图，$D$，$E$分别是$\triangle ABC$的边$AC$，$AB$上的点，$AE = 1.5$，$AC = 2$，$BC = 3$，且$\frac{AD}{AB} = \frac{3}{4}$，则$DE$的长为________.
　　　　　

答案： $\frac{9}{4}$【解析】$\because AE = 1.5$，$AC = 2$，$\therefore\frac{AE}{AC}=\frac{1.5}{2}=\frac{3}{4}$. $\because\frac{AD}{AB}=\frac{3}{4}$，$\therefore\frac{AE}{AC}=\frac{AD}{AB}$. 又$\because\angle EAD=\angle CAB$，$\therefore\triangle AED\sim\triangle ACB$，$\therefore\frac{DE}{BC}=\frac{AD}{AB}=\frac{3}{4}$，$\therefore DE=\frac{9}{4}$. 故答案为：$\frac{9}{4}$.

13. 如图，在直角三角形纸片$ABC$中，$\angle ACB = 90^{\circ}$，$AC = 10$cm. 先沿$BC$边裁剪一个宽为$4$cm的矩形纸片$PDHC$，再沿$AC$边裁剪一个边长为$4$cm的正方形纸片$QEFH$，点$D$，$E$均在$AB$边上，则$BC =$________cm.

答案： 20【解析】由题意得，$FH = CH = EF = 4\ cm$，$\therefore\angle AFE = 90^{\circ}$. $\because AC = 10\ cm$，$\therefore AF = 10 - 4 - 4 = 2(cm)$. $\because\angle AFE=\angle C = 90^{\circ}$，$\therefore EF// BC$，$\therefore\triangle AEF\sim\triangle ABC$，$\therefore\frac{AF}{AC}=\frac{EF}{BC}$，即$\frac{2}{10}=\frac{4}{BC}$，$\therefore BC = 20\ cm$. 故答案为：$20$.

14. 如图，一次函数$y = kx - 3$的图象交$x$轴于点$A$，交$y$轴于点$D$，与反比例函数$y = \frac{6}{x}(x＞0)$的图象交于点$B$，$BC$垂直$x$轴于点$C$，若$\triangle ABC$的面积为$2$，则$k$的值是________.

答案：
9【解析】如图，连接$OB$，则$S_{\triangle OBC}=\frac{1}{2}×6 = 3$.

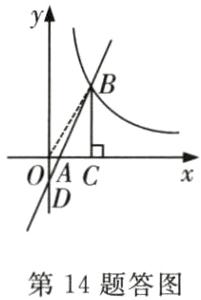
又$\because\triangle ABC$的面积为$2$，$\therefore S_{\triangle AOB}=3 - 2 = 1$，$\therefore\frac{OA}{AC}=\frac{1}{2}$. 由题知，$D(0,-3)$，$\therefore OD = 3$. $\because\angle AOD=\angle ACB = 90^{\circ}$，$\angle OAD=\angle CAB$，$\therefore\triangle AOD\sim\triangle ACB$，$\therefore\frac{OA}{AC}=\frac{OD}{BC}=\frac{1}{2}$，$\therefore BC = 2OD = 6$，$\therefore OC = 1$，$\therefore OA=\frac{1}{3}OC=\frac{1}{3}$，即点$A(\frac{1}{3},0)$，代入$y = kx - 3$得，$\frac{1}{3}k - 3 = 0$，解得$k = 9$. 故答案为：$9$.