《2025年夺冠百分百新导学课时练九年级数学下册人教版》

5.（秦皇岛卢龙期末）如图，点$A$在反比例函数$y=\frac{k}{x}$的图象上，$AB⊥x$轴于点$B$，点$C$在$x$轴上，且$CO:OB = 2:1$。$\triangle ABC$的面积为6，则$k$的值为( )

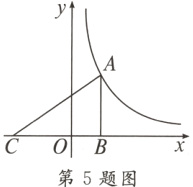
A. 2
B. 3
C. 4
D. 5

答案： C

6. 一次函数$y_1 = -x + 6$与反比例函数$y_2=\frac{8}{x}(x＞0)$的图象如图所示，当$y_1＞y_2$时，自变量$x$的取值范围是________。

答案： 2＜x＜4

7. 如图，$A$是反比例函数$y=-\frac{4}{x}$的图象上一点，过点$A$作$AB⊥y$轴于点$B$，$P$是$x$轴上的一个动点，则$\triangle ABP$的面积为________。

答案： 2

8. 已知一次函数$y = kx + b(k≠0)$的图象经过$A(3,18)$和$B(-2,8)$两点。
(1) 求一次函数的解析式。
(2) 若一次函数$y = kx + b(k≠0)$的图象与反比例函数$y=\frac{m}{x}(m≠0)$的图象只有一个交点，求交点坐标。

答案： 解：
(1) 把 $(3,18)$，$(-2,8)$ 代入一次函数 $y = kx + b(k \neq 0)$，得 $\begin{cases}3k + b = 18 \\ -2k + b = 8 \end{cases}$，解得 $\begin{cases}k = 2 \\ b = 12 \end{cases}$.
∴一次函数的解析式为 $y = 2x + 12$.
(2)
∵一次函数 $y = kx + b(k \neq 0)$ 的图象与反比例函数 $y = \frac{m}{x}(m \neq 0)$ 的图象只有一个交点，
∴$\begin{cases}y = 2x + 12 \\ y = \frac{m}{x} \end{cases}$ 只有一组解，即 $2x^2 + 12x - m = 0$ 有两个相等的实数根，
∴$\Delta = 12^2 - 4 \times 2 \times (-m) = 0$，
∴$m = -18$，$x = \frac{-12}{2 \times 2} = -3$. 把 $x = -3$ 代入 $y = 2x + 12$ 得 $y = 6$，即所求的交点坐标为 $(-3,6)$.

9.（石家庄长安区一模）如图，直线$y = 2x + 2$及反比例函数$y=\frac{k}{x}(x＞0)$的图象与两坐标轴之间的阴影部分（不包括边界）有5个整点（横、纵坐标都为整数），则$k$的取值可能是( )

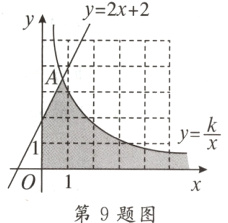
A. 2
B. 3
C. 4
D. 5

答案： C

10.（福建中考）如图，在平面直角坐标系中，反比例函数$y=\frac{k}{x}$的图象与$\odot O$交于$A$，$B$两点，且点$A$，$B$都在第一象限。若$A(1,2)$，则点$B$的坐标为________。

答案： (2,1)

11. 如图，已知一次函数$y = kx + b$的图象与反比例函数$y=\frac{m}{x}$的图象交于点$A(3,n)$和点$B(n+\frac{1}{2},2)$，与$y$轴交于点$C$。
(1) 反比例函数的解析式为________；一次函数的解析式为________。
(2) 若在$x$轴上有一点$D$，其横坐标是1，连接$AD$，$CD$，求$\triangle ACD$的面积。

答案：
解：
(1) 把点 $A(3,n)$ 和点 $B(n + \frac{1}{2},2)$ 代入 $y = \frac{m}{x}$，
得 $3n = m$，$2(n + \frac{1}{2}) = m$，解得 $n = 1$，$m = 3$，
∴$A(3,1)$，$B(\frac{3}{2},2)$，
∴反比例函数的解析式为 $y = \frac{3}{x}$；
由题意得 $\begin{cases}3k + b = 1 \\ \frac{3}{2}k + b = 2 \end{cases}$，解得 $\begin{cases}k = -\frac{2}{3} \\ b = 3 \end{cases}$，
∴一次函数的解析式为 $y = -\frac{2}{3}x + 3$.
故答案为 $y = \frac{3}{x}$，$y = -\frac{2}{3}x + 3$.
(2) 如图，作 $AE \perp x$ 轴于点 $E$，即 $E(3,0)$，

∵一次函数 $y = -\frac{2}{3}x + 3$ 的图象与 $y$ 轴交于点 $C$，
∴$C(0,3)$.
∵$D(1,0)$，
∴$DE = 2$，$OD = 1$，
∴$S_{\triangle ACD} = S_{梯形 COEA} - S_{\triangle COD} - S_{\triangle ADE} = \frac{1}{2} \times (1 + 3) \times 3 - \frac{1}{2} \times 1 \times 3 - \frac{1}{2} \times (3 - 1) \times 1 = \frac{7}{2}$.