第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
7. 如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA.
(2)若AB = 6,BC = 4,求DF的长.

(1)求证:△ABE∽△DFA.
(2)若AB = 6,BC = 4,求DF的长.

答案:
(1)证明:
∵四边形$ABCD$是矩形,
∴$AD// BC$,$\angle B = 90^{\circ}$,
∴$\angle DAF=\angle AEB$。
∵$DF\perp AE$,
∴$\angle AFD=\angle B = 90^{\circ}$,
∴$\triangle ABE\sim\triangle DFA$。
(2)解:
∵$E$是$BC$的中点,$BC = 4$,
∴$BE = 2$。
∵$AB = 6$,
∴$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{6^{2}+2^{2}}=2\sqrt{10}$。
∵四边形$ABCD$是矩形,
∴$AD = BC = 4$。
∵$\triangle ABE\sim\triangle DFA$,
∴$\frac{AB}{DF}=\frac{AE}{DA}$,
∴$DF=\frac{AB\cdot DA}{AE}=\frac{6\times4}{2\sqrt{10}}=\frac{6}{5}\sqrt{10}$。
(1)证明:
∵四边形$ABCD$是矩形,
∴$AD// BC$,$\angle B = 90^{\circ}$,
∴$\angle DAF=\angle AEB$。
∵$DF\perp AE$,
∴$\angle AFD=\angle B = 90^{\circ}$,
∴$\triangle ABE\sim\triangle DFA$。
(2)解:
∵$E$是$BC$的中点,$BC = 4$,
∴$BE = 2$。
∵$AB = 6$,
∴$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{6^{2}+2^{2}}=2\sqrt{10}$。
∵四边形$ABCD$是矩形,
∴$AD = BC = 4$。
∵$\triangle ABE\sim\triangle DFA$,
∴$\frac{AB}{DF}=\frac{AE}{DA}$,
∴$DF=\frac{AB\cdot DA}{AE}=\frac{6\times4}{2\sqrt{10}}=\frac{6}{5}\sqrt{10}$。
8. 如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆25 m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上14 cm的长度恰好遮住电线杆. 已知臂长为70 cm,则电线杆的高是( )

A. 5 m
B. 6 m
C. 125 m
D. 4 m

A. 5 m
B. 6 m
C. 125 m
D. 4 m
答案:
A
9.(数学文化)《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.
答案:
$\frac{60}{17}$
10. 如图是一个铁夹子的侧面示意图,点C是连接夹面的轴上一点,CD⊥OA于点D. 这个侧面图是轴对称图形,直线OC是它的对称轴. 已知DA = 15 mm,DO = 24 mm,DC = 10 mm. 求点A与点B之间的距离.
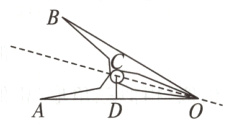

答案:
解:如图,连接$AB$交直线$OC$于点$E$。
∵这个侧面图是轴对称图形,
∴$AB\perp OC$,$AE = BE$。
∵$CD\perp OA$,
∴$OC=\sqrt{OD^{2}+CD^{2}}=\sqrt{24^{2}+10^{2}}=26(mm)$。
∵$\angle AOE=\angle COD$,
$\angle OEA=\angle ODC = 90^{\circ}$,
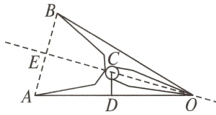
∴$\triangle OEA\sim\triangle ODC$,
∴$\frac{AE}{CD}=\frac{OA}{OC}$,
即$\frac{AE}{10}=\frac{39}{26}$,
∴$AE = 15(mm)$,
∴$AB = 2AE = 30(mm)$。
解:如图,连接$AB$交直线$OC$于点$E$。
∵这个侧面图是轴对称图形,
∴$AB\perp OC$,$AE = BE$。
∵$CD\perp OA$,
∴$OC=\sqrt{OD^{2}+CD^{2}}=\sqrt{24^{2}+10^{2}}=26(mm)$。
∵$\angle AOE=\angle COD$,
$\angle OEA=\angle ODC = 90^{\circ}$,

∴$\triangle OEA\sim\triangle ODC$,
∴$\frac{AE}{CD}=\frac{OA}{OC}$,
即$\frac{AE}{10}=\frac{39}{26}$,
∴$AE = 15(mm)$,
∴$AB = 2AE = 30(mm)$。
11. 如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若△A'B'C'的面积与△ABC的面积比是9:16,则OB':OB为( )

A. 3:4
B. 4:3
C. 7:9
D. 9:16

A. 3:4
B. 4:3
C. 7:9
D. 9:16
答案:
A
12. 在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为( )
A.(2m,2n)
B.(2m,2n)或(-2m,-2n)
C. ($\frac{1}{2}$m,$\frac{1}{2}$n)
D. ($\frac{1}{2}$m,$\frac{1}{2}$n)或(-$\frac{1}{2}$m,-$\frac{1}{2}$n)
A.(2m,2n)
B.(2m,2n)或(-2m,-2n)
C. ($\frac{1}{2}$m,$\frac{1}{2}$n)
D. ($\frac{1}{2}$m,$\frac{1}{2}$n)或(-$\frac{1}{2}$m,-$\frac{1}{2}$n)
答案:
B
13. 在平面直角坐标系中,已知点A(0,1),B(4,2),以原点O为位似中心,把△OAB按相似比$\frac{1}{2}$缩小,则点B的对应点B'的坐标是____________.
答案:
$(2,1)$或$(-2,-1)$
查看更多完整答案,请扫码查看


