第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
7.(邯郸期中)如图,在等边△ABC中,点D,E分别在边BC,AC上,∠ADE = 60°,若AD = 4,$\frac{BD}{CE}=\frac{3}{2}$,则DE的长度为( )
A. 1 B. $\frac{4}{3}$ C. 2 D. $\frac{8}{3}$

A. 1 B. $\frac{4}{3}$ C. 2 D. $\frac{8}{3}$

答案:
D
8. 如图,在Rt△ABC中,已知∠BAC = 90°,AB = AC = 2,点D在BC上运动(不能到达点B,C),过点D作∠ADE = 45°,DE交AC于点E.
(1)求证:△ABD∽△DCE.
(2)当△ADE是等腰三角形时,求AE的长.

(1)求证:△ABD∽△DCE.
(2)当△ADE是等腰三角形时,求AE的长.

答案:
(1)证明:在Rt△ABC中,∠BAC = 90°,AB = AC,
∴∠B = ∠C = 45°.
∵∠ADC = ∠B + ∠BAD,∠ADC = ∠ADE + ∠EDC,
∴∠ADE + ∠EDC = ∠B + ∠BAD.
又
∵∠ADE = 45°,
∴45° + ∠EDC = 45° + ∠BAD,
∴∠EDC = ∠BAD,
∴△ABD∽△DCE.
(2)解:
∵∠BAC = 90°,AB = AC = 2,
∴$BC=\sqrt{AB^{2}+AC^{2}} = 2\sqrt{2}$.
分三种情况讨论:
①当AD = AE时,∠DAE = 90°,此时点D与点B重合,不合题意;
②当AD = DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,则CD = AB = 2,EC = BD = BC - CD = $2\sqrt{2}-2$,AE = AC - EC = 2 - ($2\sqrt{2}-2$) = $4 - 2\sqrt{2}$;
③如图,当AE = DE时,
∠DAE = ∠ADE = 45°,
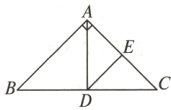
∴AD⊥BC,DE⊥AC,且AD = DC.
∴$AE = CE=\frac{1}{2}AC = 1$.
综上,可得AE = $4 - 2\sqrt{2}$或1.
(1)证明:在Rt△ABC中,∠BAC = 90°,AB = AC,
∴∠B = ∠C = 45°.
∵∠ADC = ∠B + ∠BAD,∠ADC = ∠ADE + ∠EDC,
∴∠ADE + ∠EDC = ∠B + ∠BAD.
又
∵∠ADE = 45°,
∴45° + ∠EDC = 45° + ∠BAD,
∴∠EDC = ∠BAD,
∴△ABD∽△DCE.
(2)解:
∵∠BAC = 90°,AB = AC = 2,
∴$BC=\sqrt{AB^{2}+AC^{2}} = 2\sqrt{2}$.
分三种情况讨论:
①当AD = AE时,∠DAE = 90°,此时点D与点B重合,不合题意;
②当AD = DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,则CD = AB = 2,EC = BD = BC - CD = $2\sqrt{2}-2$,AE = AC - EC = 2 - ($2\sqrt{2}-2$) = $4 - 2\sqrt{2}$;
③如图,当AE = DE时,
∠DAE = ∠ADE = 45°,

∴AD⊥BC,DE⊥AC,且AD = DC.
∴$AE = CE=\frac{1}{2}AC = 1$.
综上,可得AE = $4 - 2\sqrt{2}$或1.
9.(新概念题)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A = 40°,∠B = 60°,求证:CD为△ABC的完美分割线.
(2)如图2,在△ABC中,AC = 2,BC = $\sqrt{2}$,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形. 求完美分割线CD的长.


(1)如图1,在△ABC中,CD为角平分线,∠A = 40°,∠B = 60°,求证:CD为△ABC的完美分割线.
(2)如图2,在△ABC中,AC = 2,BC = $\sqrt{2}$,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形. 求完美分割线CD的长.


答案:
(1)证明:
∵∠A = 40°,∠B = 60°,
∴∠ACB = 80°.
∴△ABC不是等腰三角形.
∵CD平分∠ACB,
∴$∠ACD = ∠BCD=\frac{1}{2}∠ACB = 40°$.
∴∠ACD = ∠A = 40°.
∴△ACD为等腰三角形.
∵∠DCB = ∠A = 40°,∠CBD = ∠ABC,
∴△BCD∽△BAC.
∴CD为△ABC的完美分割线.
(2)解:由题意,得AC = AD = 2,设BD = x,则AB = x + 2.
∵△BCD∽△BAC,
∴$\frac{BC}{BA}=\frac{BD}{BC}$,即$\frac{\sqrt{2}}{x + 2}=\frac{x}{\sqrt{2}}$.
∴x(x + 2) = 2.
解得$x_{1}=\sqrt{3}-1$,$x_{2}=-\sqrt{3}-1$(不合题意,舍去).
∴$BD=\sqrt{3}-1$.
∵△BCD∽△BAC,
∴$\frac{CD}{AC}=\frac{BD}{BC}=\frac{\sqrt{3}-1}{\sqrt{2}}$,
∴$CD=\frac{\sqrt{3}-1}{\sqrt{2}}\times2=\sqrt{2}(\sqrt{3}-1)=\sqrt{6}-\sqrt{2}$.
∵∠A = 40°,∠B = 60°,
∴∠ACB = 80°.
∴△ABC不是等腰三角形.
∵CD平分∠ACB,
∴$∠ACD = ∠BCD=\frac{1}{2}∠ACB = 40°$.
∴∠ACD = ∠A = 40°.
∴△ACD为等腰三角形.
∵∠DCB = ∠A = 40°,∠CBD = ∠ABC,
∴△BCD∽△BAC.
∴CD为△ABC的完美分割线.
(2)解:由题意,得AC = AD = 2,设BD = x,则AB = x + 2.
∵△BCD∽△BAC,
∴$\frac{BC}{BA}=\frac{BD}{BC}$,即$\frac{\sqrt{2}}{x + 2}=\frac{x}{\sqrt{2}}$.
∴x(x + 2) = 2.
解得$x_{1}=\sqrt{3}-1$,$x_{2}=-\sqrt{3}-1$(不合题意,舍去).
∴$BD=\sqrt{3}-1$.
∵△BCD∽△BAC,
∴$\frac{CD}{AC}=\frac{BD}{BC}=\frac{\sqrt{3}-1}{\sqrt{2}}$,
∴$CD=\frac{\sqrt{3}-1}{\sqrt{2}}\times2=\sqrt{2}(\sqrt{3}-1)=\sqrt{6}-\sqrt{2}$.
查看更多完整答案,请扫码查看


