《2025年夺冠百分百新导学课时练九年级数学下册人教版》

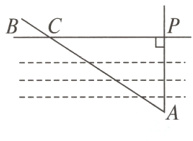
1. 如图，要测量小河两岸相对的两点P，A的距离，可以在小河边取PA的垂线PB上的一点C，测得PC = 100米，∠PCA = 35°，则小河宽PA等于( )

A. 100sin 35°米
B. 100sin 55°米
C. 100tan 35°米
D. 100tan 55°米

答案： C

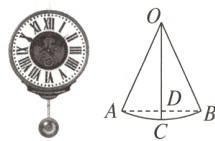
2. (邢台模拟)如图，一个钟表的摆长OA为a，当钟摆从最左侧摆到最右侧时，摆角∠AOB为2x，C是$\overset{\frown}{AB}$的中点，OC与AB交于点D，则CD的长为( )

A. $a\sin^{2}x$
B. $a\cos^{2}x$
C. $a(1 - \sin x)$
D. $a(1 - \cos x)$

答案： D

3. 数学兴趣小组利用无人机测量学校旗杆高度，已知无人机的飞行高度为40 m，当无人机与旗杆的水平距离是45 m时，观测旗杆顶部的俯角为30°，则旗杆的高度约为________ m. (结果精确到1 m，参考数据：$\sqrt{2}\approx1.41$，$\sqrt{3}\approx1.73$)

答案： 14

4. 嘉琪家对面新建了一幢图书大厦，她在自家窗口A处测得大厦顶部的仰角为45°，大厦底部的俯角为30°，如图所示，嘉琪量得两幢楼之间的距离为$20\sqrt{3}$ m.
(1)求出嘉琪家的高度AE.
(2)求出大厦的高度BD.

答案： 解：
(1)在Rt△ADE中，∠ADE = 30°，tan∠ADE = $\frac{AE}{DE}$，
∴AE = DE·tan 30° = 20$\sqrt{3}$×$\frac{\sqrt{3}}{3}$ = 20(m)，
∴嘉琪家的高度AE为20 m.
(2)
∵AC⊥BD，BD⊥DE，AE⊥DE，
∴四边形AEDC是矩形，
∴AC = DE = 20$\sqrt{3}$ m，CD = AE = 20 m.
在Rt△ABC中，∠BAC = 45°，
∴BC = AC = 20$\sqrt{3}$ m，
∴BD = BC + CD = (20$\sqrt{3}$ + 20)m.
∴大厦的高度BD为(20$\sqrt{3}$ + 20)m.