《2025年夺冠百分百新导学课时练九年级数学下册人教版》

#### 7. 如图，在□ABCD中，E是BC的中点，AE，BD相交于点O。
(1)△AOD，△EOB是否为位似图形？若是，指出其位似中心和相似比。
(2)如果S△BOE=6，求S△ABD的值。

答案： 解:
(1)△AOD与△EOB是位似图形，位似中心为O,相似比为2.
(2)在▱ABCD中,AD//BC,则△AOD∽△EOB，
∴$\frac{EO}{AO}$ = $\frac{BE}{DA}$ = $\frac{1}{2}$，
∴$\frac{S_{\triangle EOB}}{S_{\triangle AOB}}$ = $\frac{1}{2}$，$\frac{S_{\triangle EOB}}{S_{\triangle AOD}}$ = $\frac{1}{4}$.
　又$S_{\triangle BOE}$ = 6,
∴$S_{\triangle AOD}$ = 24,$S_{\triangle AOB}$ = 12,
∴$S_{\triangle ABD}$ = 36.

#### 8. 如图，在6×8网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点，以O为位似中心，在网格图中作△A'B'C'，使△A'B'C'和△ABC位似，且相似比为$\frac{1}{2}$，连接AA'，则四边形AA'C'C的周长为( )

A. 8$\sqrt{2}$
B. 6$\sqrt{2}$
C. 4$\sqrt{2}$+4
D. 6$\sqrt{2}$+4

答案： D

#### 9. 如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，△ABC与△DEF的面积之比为a：b，则$\frac{4a+3}{2b+6}$=______。

答案： $\frac{1}{2}$

#### 10. 矩形ABCD与矩形AB'C'D'是位似图形，点A为位似中心，已知矩形ABCD的周长是24，BB'=4，DD'=2，求AB和AD的长。

答案： 解:
∵矩形ABCD与矩形AB'C'D'是位似图形，且点A为位似中心，
　
∴$\frac{AB}{AB'} = \frac{AD}{AD'}$，即$\frac{AB}{AB + 4} = \frac{AD}{AD + 2}$
　
∴2AB = 4AD,即AB = 2AD.
　　又
∵矩形ABCD的周长为24，
　
∴AB + AD = 12,
　
∴AB = 8,AD = 4.

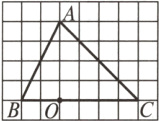
#### 11. (规律探究题)如图是由位似的正△A1B1C1，正△A2B2C2，正△A3B3C3，…，正△AnBnCn组成的图形，其中△A1B1C1的边长为1，O是B1C1的中点，A2是OA1的中点，A3是OA2的中点，…，An是OAn - 1的中点，顶点B2，B3，…，Bn，C2，C3，…，Cn都在B1C1边上。
(1)试写出正△A10B10C10和正△A7B7C7的相似比和位似中心。
(2)求出正△AnBnCn(n≥2)的周长。

答案： 解:
(1)
∵正△A₁B₁C₁的边长为1，O是B₁C₁的中点，A₂是OA₁的中点，
　
∴正△A₂B₂C₂的边长为$\frac{1}{2}$，正△A₃B₃C₃的边长为$(\frac{1}{2})^2$，…，正△A₇B₇C₇的边长为$(\frac{1}{2})^6$，正△A₁₀B₁₀C₁₀的边长为$(\frac{1}{2})^9$.
　
∴正△A₁₀B₁₀C₁₀和正△A₇B₇C₇的相似比为$\frac{(\frac{1}{2})^9}{(\frac{1}{2})^6} = \frac{1}{8}$，它们的位似中心为点O.
(2)
∵正△AₙBₙCₙ(n≥2)的边长为$(\frac{1}{2})^{n - 1}$，
　
∴正△AₙBₙCₙ(n≥2)的周长为$\frac{3}{2^{n - 1}}$.