《2025年夺冠百分百新导学课时练九年级数学下册人教版》

在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x，y)对应的位似图形上的点的坐标为________或________.

答案： $(kx,ky)$ $(-kx,-ky)$

1. (浙江中考)如图，在平面直角坐标系中，△ABC与△A'B'C'是位似图形，位似中心为点O.若点A(-3，1)的对应点为A'(-6，2)，则点B(-2，4)的对应点B'的坐标为( )

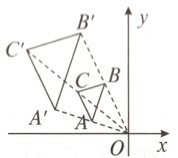
A. (-4，8)
B. (8，-4)
C. (-8，4)
D. (4，-8)

答案： A

2. 已知△ABO的顶点坐标分别为A(-1，4)，B(3，2)，O(0，0)，试将△ABO放大为△EFO，使△EFO与△ABO的相似比为2.5，其中，点E为点A的对应点，求点E和点F的坐标.

答案： 解：$\because A(-1,4),B(3,2),O(0,0)$，
$\therefore$以点$O$为位似中心，相似比为$2.5$，将$\triangle ABC$放大，则点$E$和点$F$的坐标是$(-2.5,10),(7.5,5)$或$(2.5,-10),(-7.5,-5)$。

3. 如图，在平面直角坐标系中，有一条“鱼”，它有六个顶点，则( )

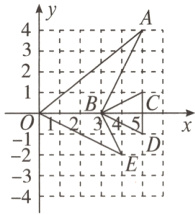
A. 将各点横坐标乘2，纵坐标不变，得到的“鱼”与原来的“鱼”位似
B. 将各点纵坐标乘2，横坐标不变，得到的“鱼”与原来的“鱼”位似
C. 将各点横、纵坐标都乘2，得到的“鱼”与原来的“鱼”位似
D. 将各点横坐标乘2，纵坐标乘$\frac{1}{2}$，得到的“鱼”与原来的“鱼”位似

答案： C

4. (石家庄高邑期中)如图，已知O是坐标原点，A，B两点的坐标分别为(3，-1)，(2，1).

(1)以点O为位似中心，在y轴的左侧将△OAB放大为原来的2倍.
(2)写出A，B两点的对应点A'，B'的坐标：A'的坐标为______，B'的坐标为______.

答案：
解：
(1)如图，$\triangle OA'B'$即为所求。
(2)$A'$的坐标为$(-6,2)$，$B'$的坐标为$(-4,-2)$。