《2025年夺冠百分百新导学课时练九年级数学下册人教版》

A 知识梳理·自主学习
(1)相似三角形对应高的比，对应中线的比与对应角平分线的比都等于________.
(2)相似三角形对应线段的比等于________.
(3)相似三角形周长的比等于相似比，相似三角形面积的比等于________.

答案： 相似比
@@相似比
@@相似比的平方

1.(石家庄桥西区期中)已知△ABC∽△A'B'C'，BD和B'D'是它们的对应中线，若$\frac{AC}{A'C'}=\frac{2}{3}$，则$\frac{BD}{B'D'}=(\ \ \ \ )$
A.$\frac{4}{9}$
B.$\frac{9}{4}$
C.$\frac{2}{3}$
D.$\frac{3}{2}$

答案： C

2.已知△ABC∽△A'B'C'，AB边上的高为2 cm，中线为2.5 cm，A'B'边上的高为8 cm，则A'B'边上的中线为( )
A.8 cm
B.9 cm
C.10 cm
D.12 cm

答案： C

3.如图，光源P在横杆AB的正上方，AB在灯光下的影子为CD，AB//CD，AB = 2 m，CD = 6 m，点P到CD的距离是2.7 m，则AB与CD间的距离是________m.

答案： 1.8

4.(唐山路北区期末)已知△ABC与△A₁B₁C₁相似，且相似比为$\frac{3}{2}$，则△ABC与△A₁B₁C₁的周长比为( )
A.1∶1
B.3∶2
C.6∶2
D.9∶4

答案： B

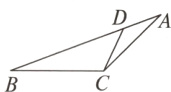
5.(秦皇岛卢龙期中)如图，△ABC∽△ACD，相似比为2，则面积之比S_{△BDC}∶S_{△DAC}为( )

A.4∶1
B.3∶1
C.2∶1
D.1∶1

答案： B

6.如图，已知在□ABCD中，AE∶EB = 1∶2.
(1)求△AEF与△CDF的周长比.
(2)如果S_{△AEF}= 6 cm²，求S_{△CDF}.

答案： 解:
(1)
∵四边形ABCD是平行四边形，
∴AB//CD，AB = CD，
∴△AEF∽△CDF.
∵AE:EB = 1:2，
∴AE:AB = 1:3，
∴AE:CD = 1:3，
∴△AEF与△CDF的周长比为1:3.
(2)
∵△AEF∽△CDF，
∴S_{△AEF}:S_{△CDF}=1:9.
∵S_{△AEF}=6cm²，
∴S_{△CDF}=6×9 = 54(cm²).