《2025年金考卷名师名题单元双测卷数学必修第一册人教版B》

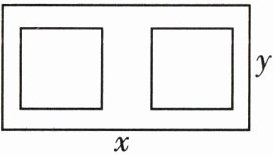
16.(15分)(教材变式)[2024江苏省徐州市高一期中]如图所示，某公益广告公司拟在一张矩形海报纸上设计大小相等的左右两个矩形宣传栏，宣传栏的面积之和为450 dm²，为了美观，要求海报上四周空白的宽度为1 dm，两个宣传栏之间的空隙的宽度为2 dm，设海报纸的长和宽分别为x dm，y dm.

(1)求y关于x的函数表达式；
(2)为节约成本，应如何选择海报纸的尺寸，可使用纸量最少？

答案：
(1)由题知，两个矩形宣传栏的长为$\frac{x - 4}{2}$，宽为$y - 2$， 所以有$2\times\frac{x - 4}{2}\times(y - 2)=450$， 整理得$y=\frac{450}{x - 4}+2(x\gt4)$.
(2)由
(1)知$(x - 4)(y - 2)=450$，即$xy = 2x + 4y + 442$， 因为$x\gt4$，$y\gt2$，所以由均值不等式可得$xy = 2x + 4y + 442\geq4\sqrt{2xy}+442$. 令$t=\sqrt{xy}$，则$t^{2}-4\sqrt{2}t - 442\geq0$，解得$t\leq - 13\sqrt{2}$（舍去）或$t\geq17\sqrt{2}$. 所以$xy\geq578$，当且仅当$\begin{cases}2x = 4y\\xy = 578\end{cases}$，即$x = 34$，$y = 17$时等号成立， 所以海报纸长34 dm，宽17 dm时，用纸量最少，最少用纸量为578 dm².