《2025年金考卷名师名题单元双测卷数学必修第一册人教版B》

13. (开放创新)已知函数$f(x)=ax+\frac{b}{x}(ab\neq0)$，使$f(x)$在$(0, +\infty)$上为增函数的$a$与$b$组成的有序实数对为$(a,b)$，则$(a,b)$可以是_______.(写出一个符合题意的有序实数对即可)

答案： $(1, - 1)$（答案不唯一） 当$a＞0$时，$y = ax$在$(0,+\infty)$上为增函数，当$b＜0$时，$y=\frac{b}{x}$在$(0,+\infty)$上为增函数，故当$a＞0,b＜0$时，$f(x)=ax+\frac{b}{x}(ab\neq0)$在$(0,+\infty)$上为增函数，故$a$可取1，$b$可取 - 1，故答案可以为$(1, - 1)$。

14. 已知函数$f(x)=\begin{cases}ax^{2}+4x,x\geq0\\ -x^{2}-bx,x ＜ 0\end{cases}$是定义在R上的偶函数，则$a + b =$__________；若对于任意的$x\in[ -2,2]$，不等式$f(x) ＜ c$恒成立，则实数$c$的取值范围为________.(本题第一空2分，第二空3分)

答案：
3 $(4,+\infty)$ 分段函数的奇偶性 + 不等式恒成立问题 思路导引 根据函数$f(x)$为偶函数，利用$f( - x)=f(x)$，列出方程，求得$a,b$的值，作出函数$y = f(x)$的图象，求得函数$f(x)$的最大值，结合题意，即可求解。 由题意，函数$f(x)=\begin{cases}ax^{2}+4x,x\geq0\\-x^{2}-bx,x＜0\end{cases}$是定义在$\mathbf{R}$上的偶函数，可得$f( - x)=f(x)$，不妨设$x＞0$，则$-x＜0$，所以$-(-x)^{2}-b( - x)=ax^{2}+4x$，即$-x^{2}+bx=ax^{2}+4x$，可得$a = - 1$，$b = 4$，所以$a + b = 3$。所以函数$f(x)=\begin{cases}-x^{2}+4x,x\geq0\\-x^{2}-4x,x＜0\end{cases}$，作出函数$y = f(x)$的图象，如图所示，可知函数$y = f(x)$的最大值为$f( - 2)=f(2)=4$，要使得对于任意的$x\in[ - 2,2]$，不等式$f(x)＜c$恒成立，则$c＞4$，所以实数$c$的取值范围为$(4,+\infty)$。 

15. (13分)已知函数$f(x)$是定义在R上的偶函数，且当$x\leq0$时，$f(x)=x^{2}+2x$，现已画出函数$f(x)$在$y$轴左侧的图象，如图所示.
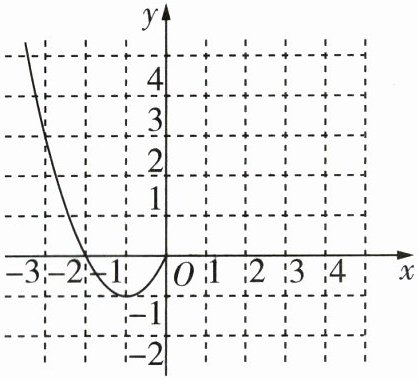
(1)请补充完整$f(x)$的图象，并写出函数$f(x)(x\in R)$的单调区间；
(2)若函数$g(x)=f(x)-(2 + 2a)x + 1(x\in[ -2, -1])$，求函数$g(x)$的最小值.

答案：
【解析】
(1)令$x＞0$，则$-x＜0$，$\therefore f( - x)=x^{2}-2x$， $\because$函数$f(x)$是定义在$\mathbf{R}$上的偶函数， $\therefore f(x)=f( - x)=x^{2}-2x$， $\therefore f(x)=\begin{cases}x^{2}+2x,x\leq0\\x^{2}-2x,x＞0\end{cases}$ (2分) 补全$f(x)$的图象，如图所示： 由函数图象可知$f(x)$的单调递增区间为$( - 1,0),(1,+\infty)$，单调递减区间为$(0,1),( - \infty, - 1)$。 (6分)
(2)第一步：确定$g(x)$的解析式 $\because g(x)=f(x)-(2 + 2a)x + 1(x\in[ - 2, - 1])$， $\therefore g(x)=x^{2}-2ax + 1$，$y=x^{2}-2ax + 1$图象的对称轴为直线$x = a$，开口向上。 (8分) 第二步：分情况讨论对称轴与区间的位置关系，进而确定函数的最小值 当$a\leq - 2$时，$g(x)_{\min}=g( - 2)=4a + 5$； 当$-2 ＜ a ＜ - 1$时，$g(x)_{\min}=g(a)=1 - a^{2}$； 当$a\geq - 1$时，$g(x)_{\min}=g( - 1)=2 + 2a$。 $\therefore g(x)_{\min}=\begin{cases}4a + 5,a\leq - 2\\1 - a^{2},-2 ＜ a ＜ - 1\\2 + 2a,a\geq - 1\end{cases}$ (13分)