2025年金考卷名师名题单元双测卷数学必修第一册人教版B
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金考卷名师名题单元双测卷数学必修第一册人教版B 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
7. [2023南通中学模拟]已知$P,Q$为$\mathbf{R}$的两个非空真子集,若$\complement_{\mathbf{R}}Q\subsetneqq\complement_{\mathbf{R}}P$,则下列结论正确的是 ( )
A. $\forall x\in Q,x\in P$
B. $\exists x\in \complement_{\mathbf{R}}P,x\in \complement_{\mathbf{R}}Q$
C. $\exists x\notin Q,x\in P$
D. $\forall x\in \complement_{\mathbf{R}}P,x\in \complement_{\mathbf{R}}Q$
A. $\forall x\in Q,x\in P$
B. $\exists x\in \complement_{\mathbf{R}}P,x\in \complement_{\mathbf{R}}Q$
C. $\exists x\notin Q,x\in P$
D. $\forall x\in \complement_{\mathbf{R}}P,x\in \complement_{\mathbf{R}}Q$
答案:
B:列表解析·直观解疑惑 因为∁RQ⊊∁RP,所以P⊊Q(题眼),用维恩图表示如图所示。 ! 根据题意,逐项分析如下:
|选项|正误|原因|
| ---- | ---- | ---- |
|A|×|因为P是Q的真子集,所以∃x∈Q, x∉P|
|B|√|因为∁RQ是∁RP的真子集且∁RQ, ∁RP都不是空集,所以∃x∈∁RP, x∈∁RQ|
|C|×|因为P是Q的真子集,所以∀x∉Q, x∉P|
|D|×|因为∁RQ是∁RP的真子集,所以∃x∈∁RP, x∉∁RQ|
根据题意,逐项分析如下:
|选项|正误|原因|
| ---- | ---- | ---- |
|A|×|因为P是Q的真子集,所以∃x∈Q, x∉P|
|B|√|因为∁RQ是∁RP的真子集且∁RQ, ∁RP都不是空集,所以∃x∈∁RP, x∈∁RQ|
|C|×|因为P是Q的真子集,所以∀x∉Q, x∉P|
|D|×|因为∁RQ是∁RP的真子集,所以∃x∈∁RP, x∉∁RQ|
B:列表解析·直观解疑惑 因为∁RQ⊊∁RP,所以P⊊Q(题眼),用维恩图表示如图所示。 !
 根据题意,逐项分析如下:
|选项|正误|原因|
| ---- | ---- | ---- |
|A|×|因为P是Q的真子集,所以∃x∈Q, x∉P|
|B|√|因为∁RQ是∁RP的真子集且∁RQ, ∁RP都不是空集,所以∃x∈∁RP, x∈∁RQ|
|C|×|因为P是Q的真子集,所以∀x∉Q, x∉P|
|D|×|因为∁RQ是∁RP的真子集,所以∃x∈∁RP, x∉∁RQ|
根据题意,逐项分析如下:
|选项|正误|原因|
| ---- | ---- | ---- |
|A|×|因为P是Q的真子集,所以∃x∈Q, x∉P|
|B|√|因为∁RQ是∁RP的真子集且∁RQ, ∁RP都不是空集,所以∃x∈∁RP, x∈∁RQ|
|C|×|因为P是Q的真子集,所以∀x∉Q, x∉P|
|D|×|因为∁RQ是∁RP的真子集,所以∃x∈∁RP, x∉∁RQ| 8. [2024福建省漳州市高一期末]已知$a,b\in \mathbf{R}$,则“$ab = 0$”的一个充分条件是 ( )
A. $a - b = 0$
B. $a + b = 0$
C. $a^{2}-b^{2}=0$
D. $a^{2}+b^{2}=0$
A. $a - b = 0$
B. $a + b = 0$
C. $a^{2}-b^{2}=0$
D. $a^{2}+b^{2}=0$
答案:
D:A(×)a - b = 0即a = b,因为a, b∈R,所以ab = 0不一定成立;B(×)a + b = 0即a = - b,因为a, b∈R,所以ab = 0不一定成立;C(×)a² - b² = 0即|a| = |b|,因为a, b∈R,所以ab = 0不一定成立;D(√)a² + b² = 0即$\begin{cases}a = 0 \\ b = 0\end{cases}$,则ab = 0成立。故选D。
9. [2024玉林十一中高一月考]已知$p$是$r$的充分不必要条件,$q$是$r$的充分条件,$s$是$r$的充要条件,$q$是$s$的必要条件,则 ( )
A. $q$是$s$的充要条件
B. $p$是$s$的充分不必要条件
C. $q$是$s$的充分不必要条件
D. $p$是$s$的充要条件
A. $q$是$s$的充要条件
B. $p$是$s$的充分不必要条件
C. $q$是$s$的充分不必要条件
D. $p$是$s$的充要条件
答案:
AB:因为p是r的充分不必要条件,q是r的充分条件,所以p⇒r, r⇏p, q⇒r。因为s是r的充要条件,所以s⇔r。因为q是s的必要条件,所以s⇒q。综上可得,q⇒r⇒s⇒q, p⇒r⇒s,但s⇔r⇏p,即q是s的充要条件,p是s的充分不必要条件,故A, B正确,C, D错误。故选AB。
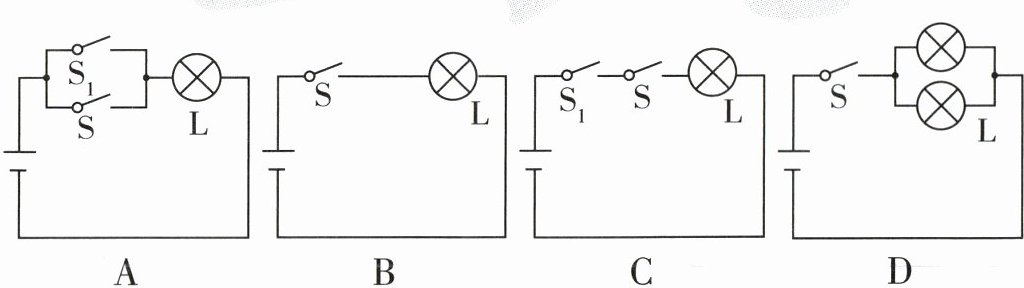
10. (学科综合) [2023东北育才学校高一开学考试]设计如图所示的四个电路图,$p$:“开关$\mathrm{S}$闭合”,$q$:“灯泡$\mathrm{L}$亮”,则$p$是$q$的充要条件的电路图是 ( )

答案:
BD:A(×)A中电路图,开关S闭合,灯泡L亮,而灯泡L亮,开关S不一定闭合,故A中p是q的充分不必要条件;B(√)B中电路图,开关S闭合,灯泡L亮,且灯泡L亮,则开关S闭合,故B中p是q的充要条件;C(×)C中电路图,开关S闭合,灯泡L不一定亮,灯泡L亮,则开关S一定闭合,故C中p是q的必要不充分条件;D(√)D中电路图,开关S闭合,则灯泡L亮,灯泡L亮,则开关S闭合,故D中p是q的充要条件。故选BD。
11. (探索创新) [2023邢台一中月考]取整函数:$[x]=$不超过$x$的最大整数,如$[1.2]=1$,$[3.9]=3$,$[-1.5]= - 2$,以下是真命题的有 ( )
A. $\forall x\in \mathbf{R},[2x]=2[x]$
B. $\forall x,y\in \mathbf{R},[x]=[y]$,则$x - y < 1$
C. $\exists x\in \mathbf{R},[2x]=2[x]$
D. $\forall x,y\in \mathbf{R},[x + y]\leq[x]+[y]$
A. $\forall x\in \mathbf{R},[2x]=2[x]$
B. $\forall x,y\in \mathbf{R},[x]=[y]$,则$x - y < 1$
C. $\exists x\in \mathbf{R},[2x]=2[x]$
D. $\forall x,y\in \mathbf{R},[x + y]\leq[x]+[y]$
答案:
BC:A(×)x = 1.5时,[2x] = [3] = 3,但2[x] = 2[1.5] = 2×1 = 2,故A为假命题;B(√)设[x] = [y] = k∈Z,则k≤x < k + 1, k≤y < k + 1,
∴ x - y < 1,故B为真命题;C(√)x = 2时,[2x] = [4] = 4 = 2[2] = 2[x],故C为真命题;D(×)x = 0.5, y = 0.6时,有[x] + [y] = 0,但[x + y] = [1.1] = 1 > [x] + [y],故D为假命题。故选BC。
∴ x - y < 1,故B为真命题;C(√)x = 2时,[2x] = [4] = 4 = 2[2] = 2[x],故C为真命题;D(×)x = 0.5, y = 0.6时,有[x] + [y] = 0,但[x + y] = [1.1] = 1 > [x] + [y],故D为假命题。故选BC。
查看更多完整答案,请扫码查看


