《2025年金考卷名师名题单元双测卷数学必修第一册人教版B》

10.[2024武汉二中高一期末]图①是某大型游乐场的游客数x(单位：万人)与收支差额y(单位：万元)的函数图象，销售初期该游乐场处于亏损状态，为了实现扭亏为盈，游乐场采取了两种措施，图②和图③中的虚线为采取了两种措施后的图象，则下列说法正确的是(收支差额 = 门票销售额 - 投入的成本费用) ( )

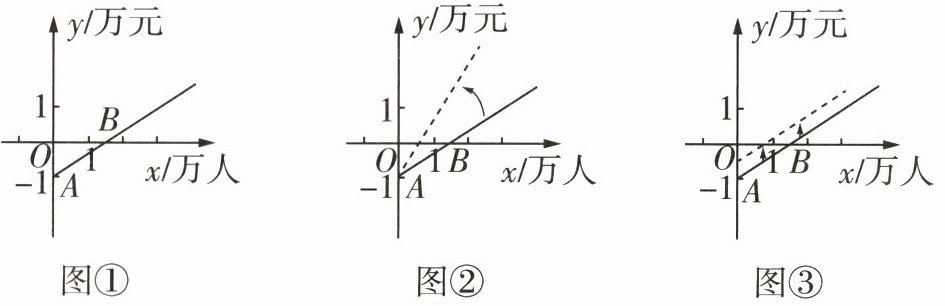
A.图①中点A的实际意义表示该游乐场投入的成本费用为1万元
B.图①中点B(1.5，0)的实际意义表示当游客数为1.5万人时，该游乐场的收支恰好平衡
C.图②游乐场实行的措施是降低门票的售价
D.图③游乐场实行的措施是减少投入的成本费用

答案： A(√)由图①中点A的坐标可知，当$x = 0$时，$y = - 1$，实际意义表示游乐场的投入成本为1万元； B(√)由图①中点B的坐标可知，当$x = 1.5$时，$y = 0$，实际意义表示当游客数为1.5万人时，游乐场的收支恰好平衡； C(×)图②中由直线与$x$轴的交点位置的变化知游乐场实行的措施是提高门票的售价； D(√)图③中由直线与$y$轴的交点位置的变化知游乐场实行的措施是减少投入的成本费用.故选ABD.

11.[2023枣庄八中期末]如图所示，一座小岛距离海岸线上最近的P点的距离是2 km，从P点沿海岸正东12 km处有一个城镇.假设一个人准备从小岛到城镇去，已知驾驶的小船的平均速度为3 km/h，步行的速度为5 km/h，t(单位：h)表示他从小岛到城镇的时间，x(单位：km)表示此人将船停在海岸处距P点的距离.设$u=\sqrt{x^{2}+4}+x$，$v=\sqrt{x^{2}+4}-x$，则 ( )

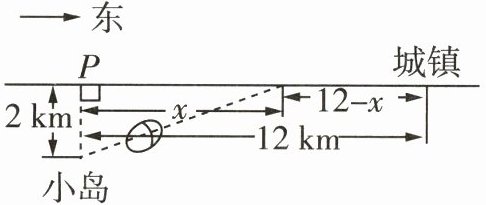
A.函数v = f(u)为减函数
B.15t - u - 4v = 32
C.当x = 1.5时，此人从小岛到城镇花费的时间最少
D.当x = 4时，此人从小岛到城镇花费的时间不超过3小时

答案： A(√)
∵$u=\sqrt{x^{2}+4}+x$，$v=\sqrt{x^{2}+4}-x$，
∴$uv = 4$，则$v=\frac{4}{u}$，又$u\geq2$，
∴$v=\frac{4}{u}$是减函数； B(×)$\sqrt{x^{2}+4}=\frac{u + v}{2}$，$x=\frac{u - v}{2}$，
∴$t=\frac{\sqrt{x^{2}+4}}{3}+\frac{12 - x}{5}=\frac{u + v}{6}+\frac{12}{5}-\frac{u - v}{10}$，整理得$15t = u + 4v + 36$，即$15t - u - 4v = 36$； C(√)由A、B得$15t = u+\frac{16}{u}+36\geq2\sqrt{u\cdot\frac{16}{u}}+36 = 44$，当且仅当$u=\frac{16}{u}$，即$u = 4$时取等号，由$\sqrt{x^{2}+4}+x = 4$，解得$x = 1.5$； D(×)$x = 4$时，$t=\frac{2\sqrt{5}}{3}+\frac{8}{5}$，$t - 3=\frac{2\sqrt{5}}{3}+\frac{8}{5}-3=\frac{10\sqrt{5}+24 - 45}{15}=\frac{10\sqrt{5}-21}{15}=\frac{\sqrt{500}-\sqrt{441}}{15}\gt0$，
∴$t\gt3$.故选AC.

12.(学科综合)[名师改编]生物学指出，生态系统中，在输入一个营养级的能量中，大约10%的能量能够流到下一个营养级，在生物链H₁→H₂→H₃→H₄中，若H₄获得10 kJ的能量，则需H₁提供的能量为________kJ.

答案： 设需$H_1$提供的能量为$x$ kJ，则$x\cdot(10\%)^3 = 10$，所以$x = 10 000$，即需$H_1$提供的能量为10 000 kJ.

13.[2023泰州中学高一期中]为了增加用户人数，某市通信公司欲下调用户的消费资费，已知该公司现有用户10万人，人均月消费50元.经测算，若人均月消费下降x%(x为正数)，则用户会增加$\frac{x}{8}$万人.若要保证该公司月总收入不减少，则x的取值范围为________.

答案： 设该公司下调用户的消费资费后的月总收入为$y$万元，则$y = 50(1-\frac{x}{100})(10+\frac{x}{8})$，要保证该公司月总收入不减少，则$50(1-\frac{x}{100})(10+\frac{x}{8})\geq10\times50$，解得$0\leq x\leq20$，又
∵$x$为正数，
∴$x$的取值范围为$(0,20]$.