2025年金考卷名师名题单元双测卷数学必修第一册人教版B
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金考卷名师名题单元双测卷数学必修第一册人教版B 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
8. [2024哈尔滨三中高一寒假验收考试]设$f(x)$是$\mathbf{R}$上的奇函数,且满足:对任意的$x_{1},x_{2}\in(-\infty,0)$且$x_{1}\neq x_{2}$都有$\frac{f(x_{1})-f(x_{2})}{x_{1}-x_{2}}<0$,$f(1)=0$,则$xf(x)<0$的解集是 ( )
A. $\{x|-1<x<0或0<x<1\}$
B. $\{x|x<-1或0<x<1\}$
C. $\{x|x<-1或x>1\}$
D. $\{x|-1<x<0或x>1\}$
A. $\{x|-1<x<0或0<x<1\}$
B. $\{x|x<-1或0<x<1\}$
C. $\{x|x<-1或x>1\}$
D. $\{x|-1<x<0或x>1\}$
答案:
C 对任意的$x_{1},x_{2}\in( -\infty,0)$且$x_{1}\neq x_{2}$都有$\frac{f(x_{1})-f(x_{2})}{x_{1}-x_{2}}<0$,所以$f(x)$在$( -\infty,0)$上单调递减,又$f(x)$是$R$上的奇函数,且$f(1)=0$,所以可以画出$f(x)$的草图如下: 要使$xf(x)<0$,则$x$与$f(x)$的符号相反,由图易知,当$x>1$时,$f(x)<0$,此时$xf(x)<0$;当$x< -1$时,$f(x)>0$,此时$xf(x)<0$。故不等式$xf(x)<0$的解集为$\{x|x< -1或x>1\}$。故选C。
要使$xf(x)<0$,则$x$与$f(x)$的符号相反,由图易知,当$x>1$时,$f(x)<0$,此时$xf(x)<0$;当$x< -1$时,$f(x)>0$,此时$xf(x)<0$。故不等式$xf(x)<0$的解集为$\{x|x< -1或x>1\}$。故选C。
C 对任意的$x_{1},x_{2}\in( -\infty,0)$且$x_{1}\neq x_{2}$都有$\frac{f(x_{1})-f(x_{2})}{x_{1}-x_{2}}<0$,所以$f(x)$在$( -\infty,0)$上单调递减,又$f(x)$是$R$上的奇函数,且$f(1)=0$,所以可以画出$f(x)$的草图如下:
 要使$xf(x)<0$,则$x$与$f(x)$的符号相反,由图易知,当$x>1$时,$f(x)<0$,此时$xf(x)<0$;当$x< -1$时,$f(x)>0$,此时$xf(x)<0$。故不等式$xf(x)<0$的解集为$\{x|x< -1或x>1\}$。故选C。
要使$xf(x)<0$,则$x$与$f(x)$的符号相反,由图易知,当$x>1$时,$f(x)<0$,此时$xf(x)<0$;当$x< -1$时,$f(x)>0$,此时$xf(x)<0$。故不等式$xf(x)<0$的解集为$\{x|x< -1或x>1\}$。故选C。 9. [2024南宁三中高一期中]已知函数$y = f(x)$的定义域为$[-1,5]$,其图象如图所示,则下列说法中正确的是 ( )
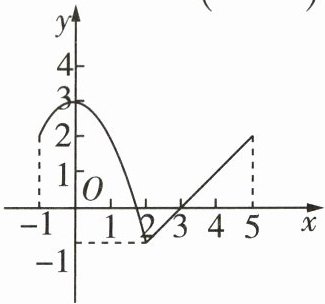
A. $f(x)$的单调递减区间为$(0,2)$
B. $f(x)$的最大值为2
C. $f(x)$的最小值为 -1
D. $f(x)$的单调递增区间为$(-1,0)$和$(2,5)$
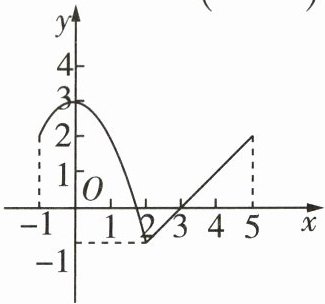
A. $f(x)$的单调递减区间为$(0,2)$
B. $f(x)$的最大值为2
C. $f(x)$的最小值为 -1
D. $f(x)$的单调递增区间为$(-1,0)$和$(2,5)$
答案:
ACD
A(√)由图象可知,$f(x)$的单调递减区间为$(0,2)$;
B(×)当$x = 0$时,$f(x)_{max}=3$;C(√)当$x = 2$时,$f(x)_{min}= -1$;D(√)由图象可知,$f(x)$的单调递增区间为$( -1,0)$和$(2,5)$。故选ACD。
10. [2024宁波效实中学高一期中]下列函数中是偶函数并且值域为$[0,+\infty )$的有 ( )
A. $f(x)=\frac{1}{x^{2}}$
B. $f(x)=|x^{2}-2|$
C. $f(x)=x^{2}+\frac{1}{x^{2}}-2$
D. $f(x)=\sqrt{x^{2}-2|x|}$
A. $f(x)=\frac{1}{x^{2}}$
B. $f(x)=|x^{2}-2|$
C. $f(x)=x^{2}+\frac{1}{x^{2}}-2$
D. $f(x)=\sqrt{x^{2}-2|x|}$
答案:
BCD
A(×)对于函数$f(x)=\frac{1}{x^{2}}$,定义域为$\{x|x\neq0\}$,值域为$(0, +\infty)$;
B(√)对于函数$f(x)=|x^{2}-2|$,定义域为$R$,且$f( -x)=|( -x)^{2}-2|=|x^{2}-2|=f(x)$,故$f(x)$为偶函数,且值域为$[0, +\infty)$;
C(√)对于函数$f(x)=x^{2}+\frac{1}{x^{2}}-2$,定义域为$\{x|x\neq0\}$,且$f( -x)=( -x)^{2}+\frac{1}{( -x)^{2}}-2=x^{2}+\frac{1}{x^{2}}-2=f(x)$,故函数$f(x)$为偶函数,又$f(x)=x^{2}+\frac{1}{x^{2}}-2\geq2\sqrt{x^{2}\cdot\frac{1}{x^{2}}}-2 = 0$,当且仅当$x=\pm1$时,等号成立,故函数$f(x)$的值域为$[0, +\infty)$;
D(√)对于函数$f(x)=\sqrt{x^{2}-2|x|}$,令$x^{2}-2|x|\geq0$,得$x = 0$或$x\geq2$或$x\leq -2$,故函数的定义域为$\{x|x = 0或x\geq2或x\leq -2\}$,关于原点对称,且$f( -x)=\sqrt{( -x)^{2}-2| -x|}=\sqrt{x^{2}-2|x|}=f(x)$,故函数$f(x)$为偶函数,且函数$f(x)$的值域为$[0, +\infty)$。故选BCD。
11. [2024青岛二中月考]函数$f(x)$满足:对任意实数$x,y$,都有$f(x + y)=f(x)+f(y)-2$,且当$x>0$时,$f(x)>2$,则 ( )
A. $f(0)=2$
B. $f(x)$的图象关于$(0,2)$对称
C. $f(-2024)+f(2024)=4$
D. $f(x)$为减函数
A. $f(0)=2$
B. $f(x)$的图象关于$(0,2)$对称
C. $f(-2024)+f(2024)=4$
D. $f(x)$为减函数
答案:
ABC
A(√)对任意实数$x$,$y$,$f(x + y)=f(x)+f(y)-2$,令$x = y = 0$,则$f(0)=f(0)+f(0)-2$,即$f(0)=2$;
B(√)令$y = -x$,则$f(0)=f(x)+f( -x)-2$,即$f(x)+f( -x)=4$;
C(√)由选项B,令$x = 2024$,得$f(2024)+f( -2024)=4$;
D(×)对任意$y\in R$,$x>0$,设$z = x + y>y$,因为当$x>0$时,$f(x)>2$,所以$f(z)-f(y)=f(x)-2>0$,即$f(z)>f(y)$,所以$f(x)$为增函数。故选ABC。
12. [2023芜湖一中高一期中]$f(x)=x^{5}+100x^{3}+x + 1$,若$f(m)=-2$,则$f(-m)=$_______.
答案:
4
令$f(x)=g(x)+1$,$g(x)=x^{5}+100x^{3}+x$,$x\in R$,则$g( -x)= -g(x)$,$g(x)$为奇函数,由$f(m)=g(m)+1 = -2$,解得$g(m)= -3$,所以$g( -m)=3$,所以$f( -m)=g( -m)+1=3 + 1 = 4$。
查看更多完整答案,请扫码查看


