《2025年北大绿卡九年级数学下册人教版》

8 如图，水杯的杯口与投影面平行，投影线的方向如箭头所示，它的正投影是( ).

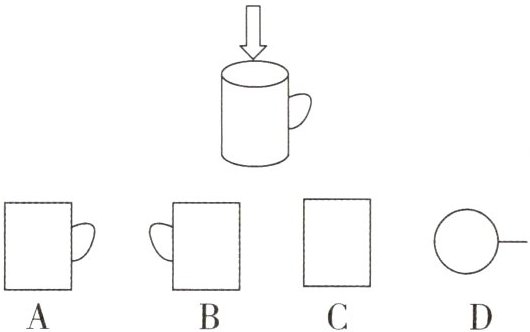
答案： D

9 当棱长为20 cm的正方体的某个面平行于投影面时，这个面的正投影的面积为( ).
A. 20 cm²
B. 300 cm²
C. 400 cm²
D. 600 cm²

答案： C

10 如图，投影线的方向如箭头所示，画出下列各图形的正投影.

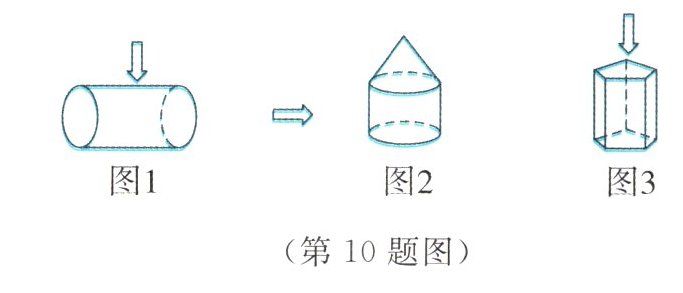
答案：
【解】如答图所示.

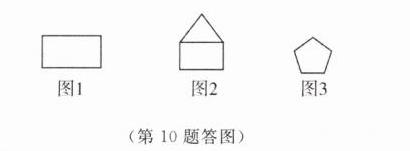
（此处应插入第10题对应的图片，图片内容为三个图形：图1是长方形，图2是上面为三角形下面为长方形的组合图形，图3是正五边形）

11 下列是描述小明和小颖在同一盏路灯下影子的图片，其中合理的是( ).

答案： D

12 在同一时刻的太阳光下，小刚的影子比小红的长，那么晚上在同一路灯下( ).
A. 小刚的影子比小红的长
B. 小红的影子比小刚的长
C. 小刚和小红的影子一样长
D. 无法确定

答案： D

13 下列投影或投影现象中，________是平行投影，________是中心投影. (只填序号)

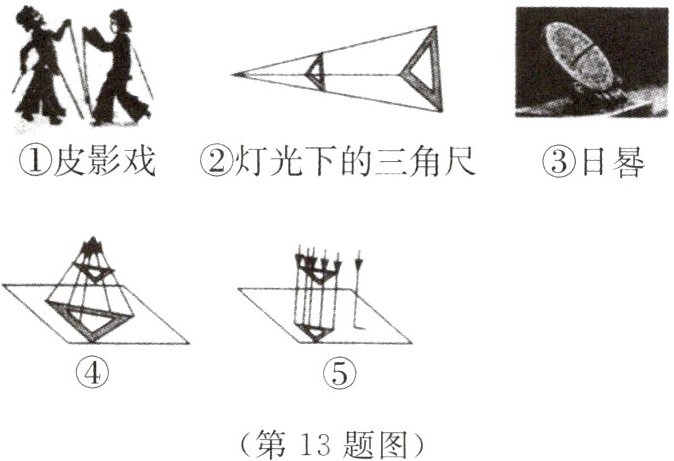
①皮影戏 ②灯光下的三角尺 ③日晷

答案： ③⑤ ①②④

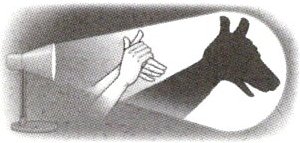
14 手影游戏利用的物理原理是：光是沿直线传播的. 图中小狗手影就是我们小时候常玩的游戏. 在一次游戏中，小明距离墙壁1米，爸爸拿着的光源与小明的距离为2米. 在小明不动的情况下，要使小狗手影的高度增加一倍，则光源与小明的距离应( ).

A. 减少\frac{3}{2}米
B. 增加\frac{3}{2}米
C. 减少\frac{5}{3}米
D. 增加\frac{5}{3}米

答案：
A 【解析】如答图1，点O为光源，AB表示小明的手，CD表示小狗手影，则AB//CD，过点O作OE⊥AB，延长OE交CD于点F，则OF⊥CD.
∵AB//CD，
∴△AOB∽△COD，则$\frac{AB}{CD}=\frac{OE}{OF}$.
∵EF = 1米，OE = 2米，
∴OF = 3米，
∴$\frac{AB}{CD}=\frac{OE}{OF}=\frac{2}{3}$.

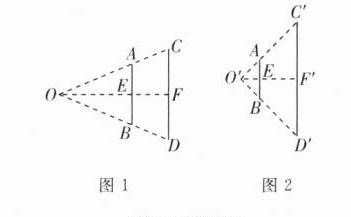
设AB = 2k，CD = 3k.
在小明不动的情况下，当小狗手影的高度增加一倍时，如答图2，
此时AB = 2k，C'D' = 6k，EF' = 1米，△AO'B∽△C'O'D'，
∴$\frac{AB}{C'D'}=\frac{O'E}{O'F'}=\frac{1}{3}$，
则O'F' - O'E = 2O'E = EF'，
∴O'E = $\frac{1}{2}$米，
∴OE - O'E = 2 - $\frac{1}{2}=\frac{3}{2}$（米），
∴光源与小明的距离变化为减少$\frac{3}{2}$米.
故选A.