《2025年北大绿卡九年级数学下册人教版》

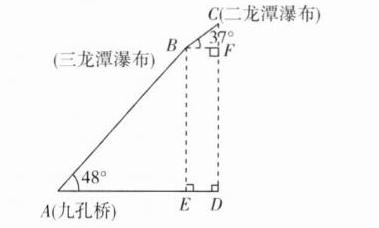
7. 渔湾是国家“AAAA”级风景区，图1是景区游览的部分示意图.如图2，小卓从九孔桥A处出发，沿着坡角为48°的山坡向上走了92 m到达B处的三龙潭瀑布，再沿坡角为37°的山坡向上走了30 m到达C处的二龙潭瀑布.求小卓从A处的九孔桥到C处的二龙潭瀑布上升的高度DC为多少米.(结果精确到0.1 m，参考数据：sin 48°≈0.74，cos 48°≈0.67，sin 37°≈0.60，cos 37°≈0.80)

答案：
【解】过点$B$作$BE\perp AD$,垂足为$E$.
在$Rt\triangle ABE$中,$\sin\angle BAE=\frac{BE}{AB}$,
$\therefore BE = AB\sin\angle BAE = 92\sin48^{\circ}\approx92\times0.74 = 68.08(m)$.
过点$B$作$BF\perp CD$,垂足为$F$.

在$Rt\triangle CBF$中,$\sin\angle CBF=\frac{CF}{BC}$,
$\therefore CF = BC\sin\angle CBF = 30\sin37^{\circ}\approx30\times0.60 = 18(m)$.
$\because FD = BE = 68.08\ m$,
$\therefore DC = FD + CF = 68.08 + 18 = 86.08\approx86.1(m)$,
$\therefore$小卓从$A$处的九孔桥到$C$处的二龙潭瀑布上升的高度$DC$约为$86.1\ m$.

8. 如图，旗杆及升旗台的剖面和教学楼的剖面在同一平面上，旗杆与地面垂直，在教学楼底部E点处测得旗杆顶端的仰角∠AED＝58°，升旗台底部到教学楼底部的距离DE＝7米，升旗台坡面CD的坡度i＝1∶0.75，坡长CD＝2米，若旗杆底部到坡面CD的水平距离BC＝1米，则旗杆AB的高度约为( )

A. 12.6米
B. 13.1米
C. 14.7米
D. 16.3米

答案： B

9. 如图，在一笔直的沿湖道路l上有A、B两个游船码头，观光岛屿C在码头A北偏东60°的方向，在码头B北偏西45°的方向，AC＝4 km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B，设开往码头A，B的游船速度分别为v₁，v₂，若回到A，B所用时间相等，则$\frac{v_{1}}{v_{2}}$＝_______.(结果用根号表示)

答案： $\sqrt{2}$

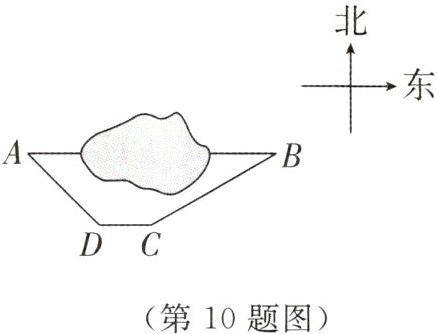
10. 如图，某景区A、B两个景点位于湖泊两侧，游客需沿着AD→DC→CB绕行才能从A景点到达B景点.经测量，D点位于A点南偏东45°方向200米处，C点在D点正东方向100米处且在B点的南偏西60°方向.当地政府为了方便游客游览，打算修建一条从A景点直达B景点的跨湖栈道AB.(结果精确到1米，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，$\sqrt{6}$≈2.449)
(1)求BC的长度；
(2)栈道修通后，从景点A到景点B走栈道比原路线少走多少米?
[img id=第10题图]

答案：
【解】
(1)过点$A$作$AE\perp CD$,交$CD$的延长线于点$E$,过点$B$作$BF\perp CD$,交$DC$的延长线于点$F$.

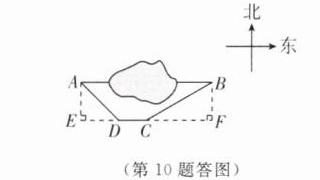
由题意得$AE = BF$.
在$Rt\triangle AED$中,$\angle EAD = 45^{\circ},AD = 200$米,
$\therefore AE = AD\cdot\cos45^{\circ}=200\times\frac{\sqrt{2}}{2}=100\sqrt{2}$(米),
$\therefore AE = BF = 100\sqrt{2}$米.
在$Rt\triangle BCF$中,$\angle CBF = 60^{\circ}$,
$\therefore BC=\frac{BF}{\cos60^{\circ}}=\frac{100\sqrt{2}}{\frac{1}{2}}=200\sqrt{2}\approx283$(米),
$\therefore BC$的长度约为$283$米.
(2)由题意得$AB = EF,CD = 100$米.
在$Rt\triangle AED$中,$\angle EAD = 45^{\circ},AD = 200$米,
$\therefore DE = AD\cdot\sin45^{\circ}=200\times\frac{\sqrt{2}}{2}=100\sqrt{2}$(米).
在$Rt\triangle BCF$中,$\angle CBF = 60^{\circ},BC = 200\sqrt{2}$米,
$\therefore CF = BC\cdot\sin60^{\circ}=200\sqrt{2}\times\frac{\sqrt{3}}{2}=100\sqrt{6}$(米),
$\therefore AB = EF = DE + DC + CF=(100\sqrt{2}+100 + 100\sqrt{6})$米.
$\because AD + CD + BC = 200 + 100 + 200\sqrt{2}=(300 + 200\sqrt{2})$(米),
$\therefore$栈道修通后,从景点$A$到景点$B$走栈道比原路线少走$300 + 200\sqrt{2}-(100\sqrt{2}+100 + 100\sqrt{6})\approx97$(米),
$\therefore$栈道修通后,从景点$A$到景点$B$走栈道比原路线少走约$97$米.