第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
10. 暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶$600$m高的山峰,由山底$A$处先步行$300$m到达$B$处,再由$B$处乘坐登山缆车到达山顶$D$处. 已知点$A$,$B$,$D$,$E$,$F$在同一平面内,山坡$AB$的坡角为$30^{\circ}$,缆车行驶路线$BD$与水平面的夹角为$53^{\circ}$(换乘登山缆车的时间忽略不计).
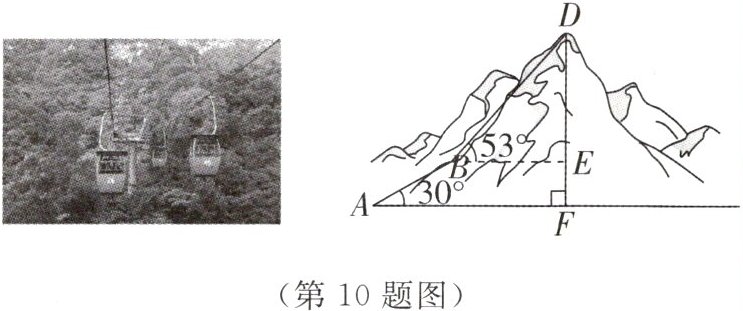
(1)求登山缆车上升的高度$DE$;
(2)若步行速度为$30$m/min,登山缆车的速度为$60$m/min,求从山底$A$处到达山顶$D$处大约需要多少分钟(结果精确到$0.1$min).
(参考数据:$\sin53^{\circ}\approx0.80$,$\cos53^{\circ}\approx0.60$,$\tan53^{\circ}\approx1.33$)

(1)求登山缆车上升的高度$DE$;
(2)若步行速度为$30$m/min,登山缆车的速度为$60$m/min,求从山底$A$处到达山顶$D$处大约需要多少分钟(结果精确到$0.1$min).
(参考数据:$\sin53^{\circ}\approx0.80$,$\cos53^{\circ}\approx0.60$,$\tan53^{\circ}\approx1.33$)
答案:
【解】
(1)如图,过$B$点作$BC\perp AF$于$C$,则四边形$BEFC$是矩形。
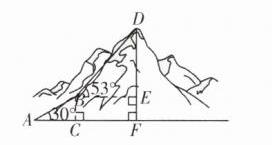
(第10题答图)
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 30^{\circ}$,$AB = 300$m,
$\therefore EF = BC=\frac{1}{2}AB = 150$m,
$\therefore DE = DF - EF = 600 - 150 = 450$(m)。
答:登山缆车上升的高度$DE$为$450$m。
(2)在$Rt\triangle BDE$中,$\angle DEB = 90^{\circ}$,$\angle DBE = 53^{\circ}$,$DE = 450$m,
$\therefore BD=\frac{DE}{\sin53^{\circ}}\approx\frac{450}{0.8}=562.5$(m),
$\therefore$从山底$A$处到达山顶$D$处大约需要
$\frac{300}{30}+\frac{562.5}{60}=19.375\approx19.4$(min)。
答:从山底$A$处到达山顶$D$处大约需要$19.4$min。
【解】
(1)如图,过$B$点作$BC\perp AF$于$C$,则四边形$BEFC$是矩形。

(第10题答图)
在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 30^{\circ}$,$AB = 300$m,
$\therefore EF = BC=\frac{1}{2}AB = 150$m,
$\therefore DE = DF - EF = 600 - 150 = 450$(m)。
答:登山缆车上升的高度$DE$为$450$m。
(2)在$Rt\triangle BDE$中,$\angle DEB = 90^{\circ}$,$\angle DBE = 53^{\circ}$,$DE = 450$m,
$\therefore BD=\frac{DE}{\sin53^{\circ}}\approx\frac{450}{0.8}=562.5$(m),
$\therefore$从山底$A$处到达山顶$D$处大约需要
$\frac{300}{30}+\frac{562.5}{60}=19.375\approx19.4$(min)。
答:从山底$A$处到达山顶$D$处大约需要$19.4$min。
11. 如图所示是某路灯在铅垂面内的示意图,灯柱$AC$的高为$11$m,灯杆$AB$与灯柱$AC$的夹角$\angle A = 120^{\circ}$,路灯采用锥形灯罩,在地面上的照射区域$DE$长为$18$m,从$D$,$E$两处测得路灯$B$的仰角分别为$\alpha$和$\beta$,且$\tan\alpha = 6$,$\tan\beta = \frac{3}{4}$,求灯杆$AB$的长度.
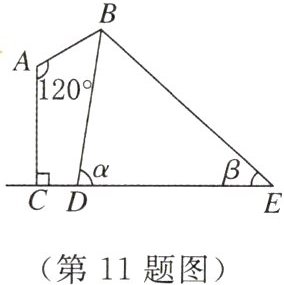

答案:
【解】过点$B$作$BF\perp CE$,交$CE$于点$F$,
过点$A$作$AG\perp BF$,交$BF$于点$G$,
则$FG = AC = 11$m。
设$DF = x$m,在$Rt\triangle BDF$中,
$\because\tan\alpha=\frac{BF}{DF}$,$\therefore BF = DF\cdot\tan\alpha = 6x$m。
在$Rt\triangle BFE$中,$\because\tan\beta=\frac{BF}{EF}$,
$\therefore EF=\frac{BF}{\tan\beta}=8x$m。
$\because DE = 18$m,$\therefore x + 8x = 18$,解得$x = 2$,$\therefore BF = 12$m,
$\therefore BG = BF - GF = 12 - 11 = 1$(m)。
$\because\angle BAC = 120^{\circ}$,
$\therefore\angle BAG=\angle BAC-\angle CAG = 120^{\circ}-90^{\circ}=30^{\circ}$,
$\therefore AB = 2BG = 2$m。
答:灯杆$AB$的长度为$2$m。
过点$A$作$AG\perp BF$,交$BF$于点$G$,
则$FG = AC = 11$m。
设$DF = x$m,在$Rt\triangle BDF$中,
$\because\tan\alpha=\frac{BF}{DF}$,$\therefore BF = DF\cdot\tan\alpha = 6x$m。
在$Rt\triangle BFE$中,$\because\tan\beta=\frac{BF}{EF}$,
$\therefore EF=\frac{BF}{\tan\beta}=8x$m。
$\because DE = 18$m,$\therefore x + 8x = 18$,解得$x = 2$,$\therefore BF = 12$m,
$\therefore BG = BF - GF = 12 - 11 = 1$(m)。
$\because\angle BAC = 120^{\circ}$,
$\therefore\angle BAG=\angle BAC-\angle CAG = 120^{\circ}-90^{\circ}=30^{\circ}$,
$\therefore AB = 2BG = 2$m。
答:灯杆$AB$的长度为$2$m。
查看更多完整答案,请扫码查看


