《2025年北大绿卡九年级数学下册人教版》

13. 如图，在平面直角坐标系中，正方形ABCD的中心在原点O，且正方形的一组对边与x轴平行，点P(2a,a)是反比例函数$y = \frac{8}{x}$的图象与正方形的一个交点，则图中阴影部分的面积是______。

答案：
16
【解析】如答图，

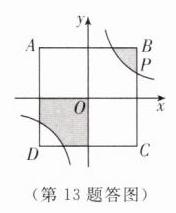
∵点 P(2a,a)在反比例函数 y = $\frac{8}{x}$的图象上，
∴2a×a = 8，解得 a = 2 或 a = -2(舍去)，
∴P(4,2).
∵正方形 ABCD 的中心为原点 O，
∴B(4,4)，
∴S_{正方形ABCD} = 8×8 = 64.
∵反比例函数图象具有中心对称性，
∴S_阴影 = $\frac{1}{4}$S_{正方形ABCD} = $\frac{1}{4}$×64 = 16.
故答案为 16.

14. 如图，一次函数$y = kx + 5$(k为常数，且$k\neq0$)的图象与反比例函数$y = -\frac{8}{x}$的图象交于A(-2,b)，B两点.
(1)求一次函数的解析式；
(2)若将直线AB沿y轴向下平移m(m＞0)个单位长度后与反比例函数的图象有且只有一个公共点，求m的值.

答案： 【解】
(1)把 A(-2,b)的坐标代入 y = -$\frac{8}{x}$，
得 b = -$\frac{8}{-2}$ = 4，
∴A 点坐标为(-2,4).
把 A(-2,4)的坐标代入 y = kx + 5，得 -2k + 5 = 4，
解得 k = $\frac{1}{2}$，
∴一次函数的解析式为 y = $\frac{1}{2}$x + 5.
(2)设平移后直线的解析式为 y = $\frac{1}{2}$x + 5 - m，
根据题意，列方程组$\begin{cases}y = -\frac{8}{x} \\y = \frac{1}{2}x + 5 - m\end{cases}$，
整理，得$\frac{1}{2}$x² - (m - 5)x + 8 = 0，
Δ = (m - 5)² - 4×$\frac{1}{2}$×8 = 0，
即(m - 5)² = 16，解得 m = 9 或 m = 1，
即 m 的值为 1 或 9.

15. 如图1，在平面直角坐标系xOy中，一次函数$y = kx + 1(k\neq0)$的图象与反比例函数$y = \frac{6}{x}$的图象交于A，B两点，与y轴交于点C，点A的横坐标为2.
(1)求k的值；
(2)利用图象直接写出$kx + 1＜\frac{6}{x}$时x的取值范围；
(3)如图2，将直线AB沿y轴向下平移4个单位，与函数$y = \frac{6}{x}(x＞0)$的图象交于点D，与y轴交于点E，再将函数$y = \frac{6}{x}(x＞0)$的图象沿AB平移，使点A，D分别平移到点C，F处，求图中阴影部分的面积.

答案：
【解】
(1)
∵点 A 在 y = $\frac{6}{x}$的图象上，
∴当 x = 2 时，y = $\frac{6}{2}$ = 3，
∴A(2,3)，
将点 A(2,3)代入 y = kx + 1，得 k = 1.
(2)由
(1)知，y = x + 1，
联立$\begin{cases}y = x + 1 \\y = \frac{6}{x}\end{cases}$，解得$\begin{cases}x = 2 \\y = 3\end{cases}$或$\begin{cases}x = -3 \\y = -2\end{cases}$，
∴B(-3,-2).
由图象可得，kx + 1＜$\frac{6}{x}$时 x 的取值范围为 x＜-3 或 0＜x＜2.
(3)
∵y = x + 1，
∴当 x = 0 时，y = 1，
∴C(0,1).
∵将直线 AB 沿 y 轴向下平移 4 个单位，
∴CE = 4，直线 DE 的解析式为 y = x - 3.
设直线 DE 与 x 轴交于点 H，
∴当 x = 0 时，y = -3，当 y = 0 时，x = 3，
∴H(3,0)，E(0,-3)，
∴OH = OE = 3，
∴∠FEC = 45°.
如答图，过点 C 作 CG⊥DE，垂足为 G，
∴CG = $\frac{\sqrt{2}}{2}$CE = 2$\sqrt{2}$.
又
∵A(2,3)，C(0,1)，
∴AC = 2$\sqrt{2}$.
连接 AD，CF，
由平移性质可知，阴影部分面积等于□ACFD 的面积，
即 2$\sqrt{2}$×2$\sqrt{2}$ = 8.