《2025年北大绿卡九年级数学下册人教版》

1. 如图，取一根长100 cm的匀质木杆，用细绳绑在木杆的中点O并将其吊起来，在中点O的左侧距离中点O 25 cm($L_{1}=25$ cm)处挂一个重9.8 N($F_{1}=9.8$ N)的物体，在中点O的右侧用一个弹簧秤向下拉，使木杆处于水平状态. 弹簧秤与中点O的距离L(单位：cm)及弹簧秤的示数F(单位：N)满足$FL = F_{1}L_{1}$. 以L的数值为横坐标，F的数值为纵坐标建立直角坐标系. 则F关于L的函数图象大致是( ).

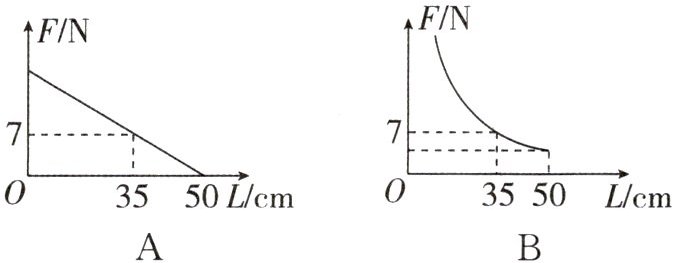
答案： B

2. 某闭合电路中，电源的电压为定值，电流I(A)与电阻R(Ω)成反比例. 如图所示的是该电路中电流I与电阻R之间函数关系的图象，当电阻R为6 Ω时，电流I为________ A.
[img id=第2题图]

答案： 1

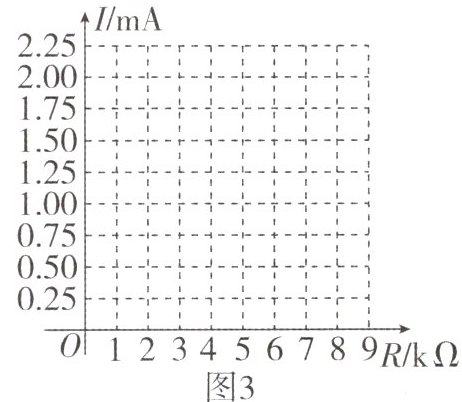
3. 数学兴趣小组了解到一款如图1所示的电子托盘秤，它是通过所称重物调节可变电阻R的大小，从而改变电路中的电流I，最终通过显示器显示物体质量. 已知可变电阻R(单位：kΩ)与物体质量m(单位：kg)之间的关系如图2所示，电流I(单位：mA)与可变电阻R之间的关系为$I = \frac{6}{R + 3}(R\geq0)$.
(1)该小组先探究函数$I = \frac{6}{R + 3}(R\geq0)$的图象与性质，并根据I与R之间关系得到如下表格：
|$R$(kΩ)|0|1|2|3|4|5|6|7|…|
|$I$(mA)|2|1.5|1.2|$p$|0.75|0.6| | | |
①表格中的$p =$________；
②请在图3中画出$I = \frac{6}{R + 3}(R\geq0)$对应的函数图象.
(2)该小组综合图2和图3发现，I随着m的增大而________(填“增大”或“减小”).
(3)若将该款电子秤中的电路电流范围设定为0.2 ＜ I ≤ 0.4(单位：mA)，判断该电子托盘秤能否称出质量为2 kg的物体的质量? 请说明理由.
[img id=图1] [img id=图2] [img id=图3]

答案：
【解】
(1)①$\because I = \frac{6}{R + 3}(R\geq0)$，
$\therefore$当$R = 3$时，$I = \frac{6}{3 + 3} = 1(\text{mA})$. 故答案为 1.
②描点，连线，如图：

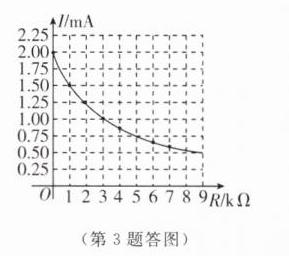
(第 3 题答图)
(2)观察图象可知，电流$I$随可变电阻$R$的增大而减小，可变电阻$R$随物体质量$m$的增大而减小，
故电流$I$随物体质量$m$的增大而增大，
故答案为增大.
(3)不能，理由如下：
当电流取最大为$0.4\text{ mA}$时，电子秤所称重的质量最大，此时$R$接入电阻值最小，
即$\frac{6}{R + 3} = 0.4$，$\therefore R = 12(\text{k}\Omega)$.
设$R = km + b$，
当$m = 0$时，$R = 24$，代入，得$b = 24$，
当$m = 3$时，$R = 0$，代入，得$3k + 24 = 0$，解得$k = - 8$，
$\therefore R$与$m$的关系式为$R = - 8m + 24$.
当$R = 12$时，$12 = - 8m + 24$，
解得$m = 1.5$，
即电子体重秤可称的最大质量为$1.5\text{ kg}$，
$\therefore$该电子托盘秤不能称出质量为$2\text{ kg}$的物体的质量.