《2025年北大绿卡九年级数学下册人教版》

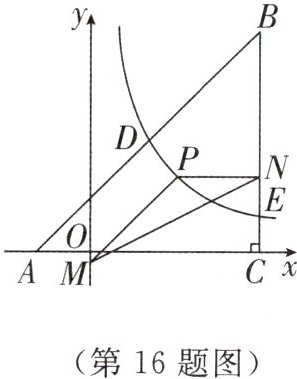
16. 如图，在△ABC中，$AC = BC$，$\angle ACB = 90^{\circ}$，A(-2,0)，C(6,0)，反比例函数$y = \frac{k}{x}(k\neq0,x＞0)$的图象与AB交于点D(m,4)，与BC交于点E.
(1)求m，k的值；
(2)点P为反比例函数$y = \frac{k}{x}(k\neq0,x＞0)$图象上一动点(点P在D，E之间运动，不与D，E重合)，过点P作PM//AB，交y轴于点M，过点P作PN//x轴，交BC于点N，连接MN，求△PMN面积的最大值，并求出此时点P的坐标.

答案：
【解】
(1)
∵A(-2,0)，C(6,0)，
∴AC = 8.
又
∵AC = BC，
∴BC = 8.
∵∠ACB = 90°，
∴点 B(6,8).
设直线 AB 的函数解析式为 y = ax + b，
将 A(-2,0)，B(6,8)代入 y = ax + b，得$\begin{cases}-2a + b = 0 \\6a + b = 8\end{cases}$，
解得$\begin{cases}a = 1 \\b = 2\end{cases}$，
∴直线 AB 的函数解析式为 y = x + 2.
将点 D(m,4)代入 y = x + 2，得 m = 2，
∴D(2,4).
将 D(2,4)代入 y = $\frac{k}{x}$，得 k = 8.
(2)延长 NP 交 y 轴于点 Q，交 AB 于点 L，如答图.

∵AC = BC，∠BCA = 90°，
∴∠BAC = 45°.
∵PN//x 轴，
∴∠BLN = ∠BAC = 45°，∠NQM = 90°.
∵PM//AB，
∴∠MPL = ∠BLP = 45°，
∴∠QMP = ∠QPM = 45°，
∴QM = QP.
设点 P 的坐标为(t,$\frac{8}{t}$)(2＜t＜6)，
则 PQ = t，PN = 6 - t，
∴MQ = PQ = t，
∴S_△PMN = $\frac{1}{2}$×PN×MQ = $\frac{1}{2}$×(6 - t)×t = -$\frac{1}{2}$(t - 3)² + $\frac{9}{2}$，
∴当 t = 3 时，S_△PMN有最大值$\frac{9}{2}$，此时 P(3,$\frac{8}{3}$).