《2025年北大绿卡九年级数学下册人教版》

17. 若锐角θ满足sin θ = 0.8，则以下结论正确的是（ ）.
A. 0°＜θ＜30°
B. 30°＜θ＜45°
C. 45°＜θ＜60°
D. 60°＜θ＜90°

答案： C 【解析】$\because\sin30^{\circ}=\frac{1}{2}$，$\sin45^{\circ}=\frac{\sqrt{2}}{2}$，$\sin60^{\circ}=\frac{\sqrt{3}}{2}$，
$\therefore$正弦值随着角度（该角度为锐角）的增大而增大，$\sin60^{\circ}=\frac{\sqrt{3}}{2}\approx0.87$，$\sin45^{\circ}=\frac{\sqrt{2}}{2}\approx0.71$，
$\therefore45^{\circ}＜\theta＜60^{\circ}$.
故选C.

18. 已知∠A为锐角，且tan A = $\sqrt{3}$，求sin²A + 2sin A·cos A + cos²A的值.

答案： 【解】$\because\angle A$为锐角，且$\tan A=\sqrt{3}$，$\therefore\angle A = 60^{\circ}$，
$\therefore$原式$=(\frac{\sqrt{3}}{2})^2+2\times\frac{\sqrt{3}}{2}\times\frac{1}{2}+(\frac{1}{2})^2=1+\frac{\sqrt{3}}{2}$.

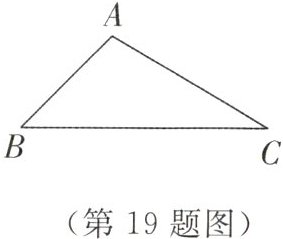
19. 如图，在△ABC中，∠BAC = 105°，∠C = 30°，AC = 2$\sqrt{3}$.求BC的长.

答案：
【解】如图所示，过点$A$作$AD\perp BC$于$D$，
$\therefore\angle ADC=\angle ADB = 90^{\circ}$.
$\because\angle C = 30^{\circ}$，$\therefore AD=\frac{1}{2}AC=\sqrt{3}$，
$\therefore CD=\sqrt{AC^{2}-AD^{2}} = 3$.
$\because\angle BAC = 105^{\circ}$，$\angle DAC = 90^{\circ}-30^{\circ}=60^{\circ}$，
$\therefore\angle BAD = 45^{\circ}$，$\therefore\triangle BAD$是等腰直角三角形，
$\therefore BD = AD=\sqrt{3}$，$\therefore BC = BD+CD = 3+\sqrt{3}$.

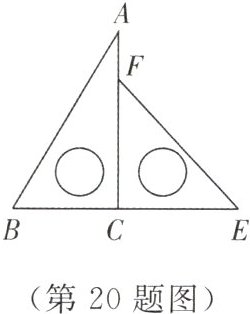
20. 数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含45°角的三角板的斜边与含30°角的三角板的长直角边相等. 于是，小陆同学提出一个问题：如图，将一副三角板的直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC = 2，求AF的长. 请你运用所学的数学知识解决这个问题.

答案： 【解】$\because$在$Rt\triangle ABC$中，$BC = 2$，$\angle A = 30^{\circ}$，
$\therefore AC=\frac{BC}{\tan A}=2\sqrt{3}$，
则$EF = AC = 2\sqrt{3}$.
$\because\angle E = 45^{\circ}$，$\therefore FC = EF\cdot\sin E=\sqrt{6}$，
$\therefore AF = AC - FC = 2\sqrt{3}-\sqrt{6}$.

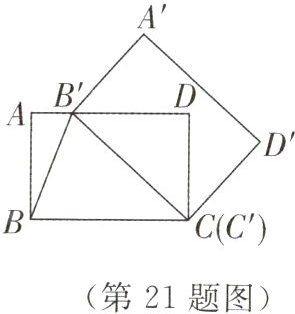
21. 如图，在矩形ABCD中，BC = 4，将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′，设旋转角为α，此时点B′恰好落在边AD上，连接B′B.
（1）当B′恰好是AD的中点时，求旋转角α的大小；
（2）若∠AB′B = 75°，求AB的长.

答案： 【解】
(1)在矩形$ABCD$中，$BC = 4$，则$AD = BC = 4$，$AB = CD$，$\angle D=\angle BCD = 90^{\circ}$.
由旋转的性质，得$BC = B'C = 4$，$\angle BCB'=\alpha$.
$\because B'$是$AD$的中点，$\therefore B'D=\frac{1}{2}AD = 2$，
即$B'D=\frac{1}{2}B'C$.
$\because\angle D = 90^{\circ}$，$\therefore\sin\angle B'CD=\frac{B'D}{B'C}=\frac{1}{2}$，
$\therefore\angle B'CD = 30^{\circ}$，
$\therefore\alpha=\angle BCB' = 90^{\circ}-\angle B'CD = 60^{\circ}$.
(2)$\because$在矩形$ABCD$中，$AD// BC$，$\angle D = 90^{\circ}$，
$\therefore\angle B'BC=\angle AB'B = 75^{\circ}$.
由旋转的性质，得$BC = B'C = 4$，
$\therefore\angle B'BC=\angle BB'C = 75^{\circ}$，
$\therefore\angle DB'C = 180^{\circ}-\angle AB'B-\angle BB'C = 30^{\circ}$.
$\because\angle D = 90^{\circ}$，$\therefore CD=\frac{1}{2}B'C = 2$，
$\therefore AB = CD = 2$.