《2025年北大绿卡九年级数学下册人教版》

9 菱湖镇某养鱼专业户准备挖一个占地形状为长方形，面积为2 000平方米的鱼塘.
(1)求鱼塘的长$y$(米)关于宽$x$(米)的函数解析式(不考虑自变量取值范围).
(2)由于受场地的限制，鱼塘的宽最多只能挖20米，当鱼塘的宽是20米时，鱼塘的长为多少米?

答案： 【解】
(1)由长方形面积为2000平方米，得到$xy = 2000$，即$y = \frac{2000}{x}$。
(2)当$x = 20$时，$y = \frac{2000}{20}=100$，故当鱼塘的宽度是20米时，鱼塘的长为100米。

10 若函数$y = (m + 1)x^{m^{2}+3m + 1}$是反比例函数，则$m =$( ).
A.-2
B.1
C.2或1
D.-2或-1

答案： A 【解析】由题意，得$m^{2}+3m + 1 = -1$且$m + 1\neq0$，解得$m = -2$。故答案为A。

11 若函数$y = (m + \frac{1}{2})x^{m - 2}$是反比例函数.
(1)求此反比例函数的解析式；
(2)当$x = 1$时，求$y$的值；
(3)当$y = 2$时，求$x$的值.

答案： 【解】
(1)由题意，知$m - 2 = -1$且$m+\frac{1}{2}\neq0$，$\therefore m = 1$，$\therefore y = \frac{3}{2x}$。
(2)当$x = 1$时，$y = \frac{3}{2}$。
(3)当$y = 2$时，$x = \frac{3}{4}$。

12 在平面直角坐标系中，函数$y = \frac{4}{x + 2}$的图象与坐标轴的交点个数是( ).
A.0
B.1
C.2
D.4

答案： B 【解析】当$x = 0$时，$y = \frac{4}{2}=2$，$\therefore y = \frac{4}{x + 2}$与$y$轴的交点为$(0,2)$。$\because\frac{4}{x + 2}$是分式，且当$x\neq -2$时，$\frac{4}{x + 2}\neq0$，即$y\neq0$，$\therefore y = \frac{4}{x + 2}$与$x$轴没有交点，$\therefore$函数$y = \frac{4}{x + 2}$的图象与坐标轴的交点个数是1。故选B。

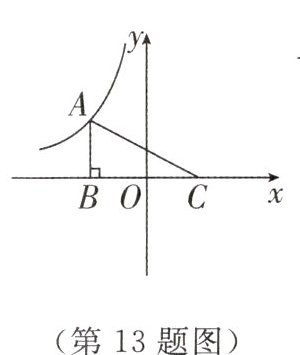
13 如图，点$A$在反比例函数$y = - \frac{10}{x}(x ＜ 0)$的图象上，$AB\perp x$轴于点$B$，$C$是点$B$关于原点$O$的对称点，连接$AC$，则$\triangle ABC$的面积为________.

答案： 10 【解析】设$A(a,b)$，则$B(a,0)$，$C(-a,0)$，$\therefore AB = b$，$BC = |2a|=-2a$，$\therefore S_{\triangle ABC}=\frac{1}{2}\times AB\times BC=\frac{1}{2}b\times(-2a)=-ab$。$\because$点$A$在反比例函数$y = -\frac{10}{x}(x\lt0)$的图象上，$\therefore ab = -10$，$\therefore S_{\triangle ABC}=-ab=-(-10)=10$。故答案为10。

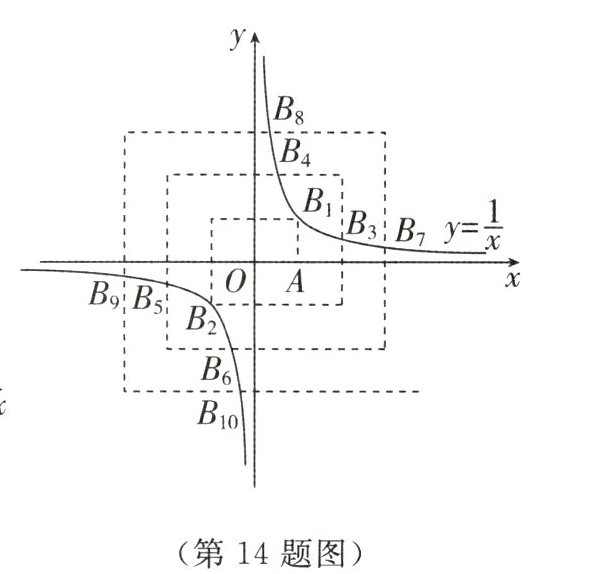
14 如图是从原点开始的通道宽度为1的回形图，$OA = 1$，反比例函数$y = \frac{1}{x}$与该回形图的交点依次记为$B_1$，$B_2$，$B_3$，$\cdots$，则$B_{2024}$的坐标为________.

答案： $(\frac{1}{507},507)$ 【解析】由题意可知，反比例函数图象上点的坐标为$(x,\frac{1}{x})$，观察图象，可以发现：第1个回形图有2个交点，$B_1(1,1)$，$B_2(-1,-1)$；第2个回形图有4个交点，分别是$B_3(2,\frac{1}{2})$，$B_4(\frac{1}{2},2)$，$B_5(-2,-\frac{1}{2})$，$B_6(-\frac{1}{2},-2)$；第3个回形图有4个交点，分别是$B_7(3,\frac{1}{3})$，$B_8(\frac{1}{3},3)$，$B_9(-3,-\frac{1}{3})$，$B_{10}(-\frac{1}{3},-3)$；…第$n(n\geq2)$个回形图有4个交点，分别是$(n,\frac{1}{n})$，$(\frac{1}{n},n)$，$(-n,-\frac{1}{n})$，$(-\frac{1}{n},-n)$。$\because(2024 - 2)\div4 = 505\cdots\cdots2$，$505 + 1+1 = 507$，$\therefore$第2024个点是第507个回形图的第2个点，$\therefore$点的坐标为$(\frac{1}{507},507)$。故答案为$(\frac{1}{507},507)$。

15 已知$y = y_1 - y_2$，并且$y_1$与$x$成正比例，$y_2$与$(x - 2)$成反比例，当$x = - 2$时，$y = - 7$；当$x = 3$时，$y = 13$.
(1)求$y$关于$x$的函数解析式；
(2)求当$x = 5$时的函数值.

答案： 【解】
(1)设$y_1 = kx$，$y_2 = \frac{m}{x - 2}$，则$y = kx-\frac{m}{x - 2}$。根据题意，得$\begin{cases}-2k-\frac{m}{-2 - 2}=-7\\3k-\frac{m}{3 - 2}=13\end{cases}$，解得$\begin{cases}k = 3\\m = -4\end{cases}$，则函数解析式是$y = 3x+\frac{4}{x - 2}$。
(2)当$x = 5$时，$y = 3\times5+\frac{4}{5 - 2}=\frac{49}{3}$。