《2025年北大绿卡九年级数学下册人教版》

1. 已知甲、乙两地相距20千米，汽车从甲地匀速行驶到乙地，则汽车行驶时间$t$(小时)关于行驶速度$v$(千米/时)的函数关系式是( )．
A. $t = 20v$
B. $t=\frac{20}{v}$
C. $t=\frac{v}{20}$
D. $t=\frac{10}{v}$

答案： B

2. 正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为$10^{5}\ m^{3}$，设土石方日平均运送量为$V$(单位：$m^{3}$/天)，完成运送任务所需要的时间为$t$(单位：天)，则$V$与$t$满足( )．
A. 反比例函数关系
B. 正比例函数关系
C. 一次函数关系
D. 二次函数关系

答案： A

3. 一台印刷机每年可印刷的书本数量$y$(万册)与它的使用时间$x$(年)成反比例关系，当$x = 2$时，$y = 20$，则$y$与$x$的函数图象大致是( )．

答案： C

4. 机器狗是一种模拟真实犬只形态和部分行为的机器装置，其最快移动速度$v$(m/s)是载重后总质量$m$(kg)的反比例函数.已知一款机器狗载重后总质量$m = 60\ kg$时，它的最快移动速度$v = 6\ m/s$；当其载重后总质量$m = 80\ kg$时，它的最快移动速度$v =$_______m/s.

答案： 4.5 【解析】设反比例函数的解析式为$v = \frac{k}{m}$，
∵机器狗载重后总质量$m = 60\ kg$时，它的最快移动速度$v = 6\ m/s$，
∴$k = 60×6 = 360$，
∴反比例函数的解析式为$v = \frac{360}{m}$。
当$m = 80\ kg$时，$v = \frac{360}{80} = 4.5(m/s)$。
故答案为 4.5。

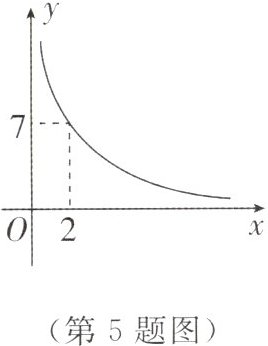
5. 经研究，某人蒙上眼睛走出的大圆圈的半径$y$与其两腿迈出的步长之差$x(x＞0)$成反比例关系，其图象如图所示.若此人蒙上眼睛后两腿迈出的步长之差为0.4，则其走出的大圆圈的半径是_______.

答案： 35 【解析】设$y$与$x$的函数解析式为$y = \frac{k}{x}(k＞0)$，
∴$7 = \frac{k}{2}$，
∴$k = 14$，
∴$y$与$x$之间的函数解析式为$y = \frac{14}{x}$。
当$x = 0.4$时，$y = 35$，
∴走出的大圆圈的半径是 35。
故答案为 35。

6. 世界的面食之根就在山西.山西面食是中华民族饮食文化中的重要组成部分.如图，厨师将一定质量的面团做成拉面时，面条的总长度$y$(m)是面条横截面面积$S(mm^{2})$的反比例函数，其图象经过$A(2,64)$，$B(m,100)$两点.
(1)求$y$与$S$之间的函数关系式；
(2)求$m$的值，并解释它的实际意义.

答案： 【解】
(1)设$y$与$S$之间的函数解析式为$y = \frac{k}{S}(S＞0)$，
将$A(2,64)$代入，得$k = 2×64 = 128$，
∴$y$与$S$之间的函数解析式为$y = \frac{128}{S}(S＞0)$。
(2)
∵点$B(m,100)$在反比例函数$y = \frac{128}{S}(S＞0)$上，
∴$100 = \frac{128}{m}$，解得$m = 1.28$，
∴$m = 1.28$，
其表示的实际意义为面条的总长度为 100 m 时，其横截面积为$1.28\ mm^{2}$。