《2025年北大绿卡九年级数学下册人教版》

1. 在Rt△ABC中，∠C = 90°，BC = 4，AC = 3，则sin B = $\frac{AC}{AB}$ = ( )
A. $\frac{3}{5}$
B. $\frac{4}{5}$
C. $\frac{3}{7}$
D. $\frac{3}{4}$

答案： A

2. 在Rt△ABC中，∠C = 90°，AB = 2BC，则sin B的值为( )
A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{2}$
D. 1

答案： C

3. 在Rt△ABC中，∠C = 90°，若△ABC的三边都放大到原来的5倍，则sin A的值( )
A. 放大到原来的5倍
B. 缩小到原来的$\frac{1}{5}$
C. 不变
D. 无法确定

答案： C

4. 如图，四边形ABCD是菱形，AC = 8，DB = 6，DE⊥AB于点E，则sin∠DAE = ( )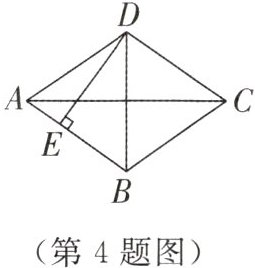
A. $\frac{2}{5}$ B. $\frac{24}{25}$C. $\frac{3}{5}$ D. $\frac{7}{25}$

答案： B

5. 如图，在△ABC中，∠C = 90°，AC：BC = 3：2，求sin A和sin B的值.
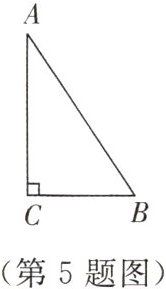
[img id=第5题图]

答案： 【解】设$AC = 3a$，则$BC = 2a$。在$Rt\triangle ABC$中，
$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{(3a)^{2}+(2a)^{2}}=\sqrt{13}a$，
$\therefore\sin A=\frac{BC}{AB}=\frac{2a}{\sqrt{13}a}=\frac{2}{13}\sqrt{13}$，
$\sin B=\frac{AC}{AB}=\frac{3a}{\sqrt{13}a}=\frac{3}{13}\sqrt{13}$。
答题要点 不要把$AC = 3$，$BC = 2$作为已知条件计算求解。

6. 在Rt△ABC中，∠C = 90°，sin A = $\frac{3}{5}$，BC = 6，则AB的长为( )
A. 4
B. 6
C. 8
D. 10

答案： D

7. 如图，P是反比例函数y = $\frac{k}{x}$ (x＞0)图象上一点，PH⊥x轴于H. 若OP = 5，sin∠POH = $\frac{3}{5}$，则k = ________.
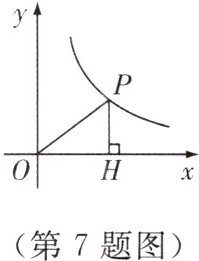
[img id=第7题图]

答案： 12

8. 如图所示，在Rt△ABC中，∠C = 90°，sin A = $\frac{4}{5}$，且BC = 20，求：
(1)sin B的值；
(2)△ABC的周长及面积.
[img id=第8题图]

答案： 【解】
(1)$\because\sin A=\frac{4}{5}$，$BC = 20$，$\therefore\sin A=\frac{20}{AB}=\frac{4}{5}$，
$\therefore AB = 20\div\frac{4}{5}=25$，
$\therefore AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{25^{2}-20^{2}}=15$，
$\therefore\sin B=\frac{AC}{AB}=\frac{15}{25}=\frac{3}{5}$。
(2)$\triangle ABC$的周长为$AB + BC + AC = 25 + 20 + 15 = 60$，
$S_{\triangle ABC}=\frac{1}{2}\times15\times20 = 150$。