《2025年北大绿卡九年级数学下册人教版》

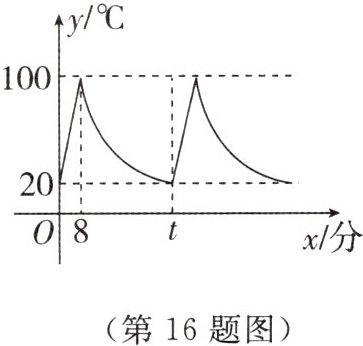
16. 小明家饮水机中原有水的温度为20 $^{\circ}C$，通电开机后，饮水机开始自动加热，此过程中水温$y(^{\circ}C)$与开机时间$x$(分)满足一次函数关系，当加热到100 $^{\circ}C$时自动停止加热，随后水温开始下降，此过程中水温$y(^{\circ}C)$与开机时间$x$(分)成反比例关系，当水温降至20 $^{\circ}C$时，饮水机又开始自动加热，…，重复上述程序(如图所示)，根据图中提供的信息，解答下列问题：
(1)当$0\leqslant x\leqslant8$时，求水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式.
(2)求图中$t$的值.
(3)有一天，小明在上午7：10(水温20 $^{\circ}C$)，开机通电后去上学，中午放学回到家时间刚好11：15，请问此时饮水机内水的温度约为多少$^{\circ}C$？并求：在7：10～11：15这段时间里，水温共有几次达到100 $^{\circ}C$？

答案： 【解】
(1)由图象可知，当$0\leq x\leq8$时是一次函数，
设$y = kx + b$，将$(0,20)$，$(8,100)$代入，得
$\begin{cases}8k + b = 100\\b = 20\end{cases}$，解得$\begin{cases}k = 10\\b = 20\end{cases}$，
∴水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式为$y = 10x + 20(0\leq x\leq8)$。
(2)在水温下降过程中，设水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式为$y = \frac{m}{x}$，
依据题意，得$100 = \frac{m}{8}$，解得$m = 800$，
∴反比例函数的解析式为$y = \frac{800}{x}$，
当$y = 20$时，$20 = \frac{800}{t}$，解得$t = 40$。
(3)由
(2)知，$t = 40$，结合图象，可知每 40 分钟图象重复出现一次，
∵$7:10～11:15$经历时间为 245 分钟，
$245\div40 = 6\cdots\cdots5$，$8 ＞ 5$，
∴当$x = 5$时，$y = 10×5 + 20 = 70(^{\circ}C)$，
答：饮水机内水温约为$70^{\circ}C$，共有 6 次达到$100\ ^{\circ}C$。