第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
13. 如图,四边形$ABCD$是某学校的一块种植实验基地,其中$\triangle ABC$是水果园,$\triangle ACD$是蔬菜园. 已知$AB// CD$,$AB = 27\ m$,$AC = 18\ m$,$CD = 12\ m$.
(1)求证:$\triangle ABC\sim\triangle CAD$;
(2)若蔬菜园$\triangle ACD$的面积为$80\ m^{2}$,求水果园$\triangle ABC$的面积.

(1)求证:$\triangle ABC\sim\triangle CAD$;
(2)若蔬菜园$\triangle ACD$的面积为$80\ m^{2}$,求水果园$\triangle ABC$的面积.

答案:
(1)【证明】$\because AB// CD$,$\therefore\angle BAC=\angle ACD$。
$\because AB = 27\ m$,$AC = 18\ m$,$CD = 12\ m$,
$\because\frac{AB}{AC}=\frac{27}{18}=\frac{3}{2}$,$\frac{AC}{CD}=\frac{18}{12}=\frac{3}{2}$,
$\therefore\frac{AB}{AC}=\frac{AC}{CD}$,$\therefore\triangle ABC\sim\triangle CAD$。
(2)【解】由
(1)知$\triangle ABC\sim\triangle CAD$,
$\therefore\frac{S_{\triangle ABC}}{S_{\triangle CAD}}=(\frac{3}{2})^2=\frac{9}{4}$,即$\frac{S_{\triangle ABC}}{80}=\frac{9}{4}$,
解得$S_{\triangle ABC}=180$。
答:水果园$\triangle ABC$的面积为$180\ m^2$。
(1)【证明】$\because AB// CD$,$\therefore\angle BAC=\angle ACD$。
$\because AB = 27\ m$,$AC = 18\ m$,$CD = 12\ m$,
$\because\frac{AB}{AC}=\frac{27}{18}=\frac{3}{2}$,$\frac{AC}{CD}=\frac{18}{12}=\frac{3}{2}$,
$\therefore\frac{AB}{AC}=\frac{AC}{CD}$,$\therefore\triangle ABC\sim\triangle CAD$。
(2)【解】由
(1)知$\triangle ABC\sim\triangle CAD$,
$\therefore\frac{S_{\triangle ABC}}{S_{\triangle CAD}}=(\frac{3}{2})^2=\frac{9}{4}$,即$\frac{S_{\triangle ABC}}{80}=\frac{9}{4}$,
解得$S_{\triangle ABC}=180$。
答:水果园$\triangle ABC$的面积为$180\ m^2$。
14. 如图1,$AD$是$\triangle ABC$的高,点$E$,$F$分别在边$AB$和$AC$上,且$EF// BC$. 由“相似三角形对应高的比等于对应边的比”可以得到以下结论:$\frac{AG}{AD}=\frac{EF}{BC}$.



(1)如图2,在$\triangle ABC$中,$BC = 6$,$BC$边上的高为$8$,在$\triangle ABC$内放一个正方形$MNGH$,使其一边$GH$在$BC$上,点$M$,$N$分别在$AB$,$AC$上,则正方形$MNGH$的边长 = _______.
(2)某葡萄酒庄欲在展厅的一面墙上布置一个腰长为$100\ cm$,底边长为$120\ cm$的等腰三角形展台. 现需将展台用平行于底边的隔板,每间隔$10\ cm$分隔出一层,再将每一层尽可能多的分隔成若干个开口为正方形的长方体格子,要求每个格子内放置一瓶葡萄酒,平面设计图如图3所示,将底边$BC$的长度看作是第0层隔板的长度.
①在分隔的过程中发现,当隔板厚度忽略不计时,每层平行于底边的隔板长度(单位:$cm$)随着层数(单位:层)的变化而变化. 请完成下表:
|层数/层|0|1|2|3|…|
|----|----|----|----|----|----|
|隔板长度/cm|120|____|____|____|…|
②在①的条件下,请直接写出该展台最多可以摆放多少瓶葡萄酒?



(1)如图2,在$\triangle ABC$中,$BC = 6$,$BC$边上的高为$8$,在$\triangle ABC$内放一个正方形$MNGH$,使其一边$GH$在$BC$上,点$M$,$N$分别在$AB$,$AC$上,则正方形$MNGH$的边长 = _______.
(2)某葡萄酒庄欲在展厅的一面墙上布置一个腰长为$100\ cm$,底边长为$120\ cm$的等腰三角形展台. 现需将展台用平行于底边的隔板,每间隔$10\ cm$分隔出一层,再将每一层尽可能多的分隔成若干个开口为正方形的长方体格子,要求每个格子内放置一瓶葡萄酒,平面设计图如图3所示,将底边$BC$的长度看作是第0层隔板的长度.
①在分隔的过程中发现,当隔板厚度忽略不计时,每层平行于底边的隔板长度(单位:$cm$)随着层数(单位:层)的变化而变化. 请完成下表:
|层数/层|0|1|2|3|…|
|----|----|----|----|----|----|
|隔板长度/cm|120|____|____|____|…|
②在①的条件下,请直接写出该展台最多可以摆放多少瓶葡萄酒?
答案:
【解】
(1)如答图1,作$AD\perp BC$于$D$,交$MN$于$E$,
由题意,得$\frac{AE}{AD}=\frac{MN}{BC}$。
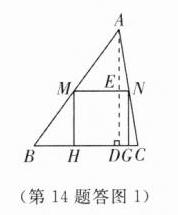
设正方形$MNGH$的边长为$x$,则
$\frac{8 - x}{8}=\frac{x}{6}$,解得$x=\frac{24}{7}$。
故答案为$\frac{24}{7}$。
(2)如答图2,作$AD\perp BC$于$D$,
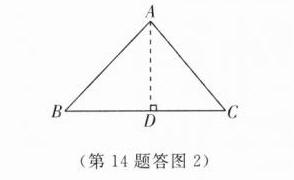
$\because AB = AC = 100\ cm$,
$\therefore BD = CD=\frac{1}{2}BC = 60\ cm$,
$\therefore AD=\sqrt{100^2 - 60^2}=80(cm)$。
①设第1层,第2层,第3层隔板的长度分别为$y_1$,$y_2$,$y_3$,则
$\frac{y_1}{120}=\frac{80 - 10}{80}$,解得$y_1 = 105$。
$\frac{y_2}{120}=\frac{80 - 20}{80}$,解得$y_2 = 90$。
$\frac{y_3}{120}=\frac{80 - 30}{80}$,解得$y_3 = 75$。
故答案为$105$,$90$,$75$。
②第$n$层隔板的长度的分别为$y_n$,则
$\frac{y_n}{120}=\frac{80 - 10n}{80}$,
解得$y_n = 120 - 15n$。
因此得$y_4 = 60$,$y_5 = 45$,$y_6 = 30$,$y_7 = 15$,
故最多可摆$7$层。
第1层可摆$105\div10 = 10.5\approx10$(瓶);
第2层可摆$90\div10 = 9$(瓶);
第3层可摆$75\div10 = 7.5\approx7$(瓶);
第4层可摆$60\div10 = 6$(瓶);
第5层可摆$45\div10 = 4.5\approx4$(瓶);
第6层可摆$30\div10 = 3$(瓶);
第7层可摆$15\div10 = 1.5\approx1$(瓶)。
共$10 + 9+7 + 6+4 + 3+1 = 40$(瓶),
故该展台最多可摆$40$瓶葡萄酒。
【解】
(1)如答图1,作$AD\perp BC$于$D$,交$MN$于$E$,
由题意,得$\frac{AE}{AD}=\frac{MN}{BC}$。

设正方形$MNGH$的边长为$x$,则
$\frac{8 - x}{8}=\frac{x}{6}$,解得$x=\frac{24}{7}$。
故答案为$\frac{24}{7}$。
(2)如答图2,作$AD\perp BC$于$D$,

$\because AB = AC = 100\ cm$,
$\therefore BD = CD=\frac{1}{2}BC = 60\ cm$,
$\therefore AD=\sqrt{100^2 - 60^2}=80(cm)$。
①设第1层,第2层,第3层隔板的长度分别为$y_1$,$y_2$,$y_3$,则
$\frac{y_1}{120}=\frac{80 - 10}{80}$,解得$y_1 = 105$。
$\frac{y_2}{120}=\frac{80 - 20}{80}$,解得$y_2 = 90$。
$\frac{y_3}{120}=\frac{80 - 30}{80}$,解得$y_3 = 75$。
故答案为$105$,$90$,$75$。
②第$n$层隔板的长度的分别为$y_n$,则
$\frac{y_n}{120}=\frac{80 - 10n}{80}$,
解得$y_n = 120 - 15n$。
因此得$y_4 = 60$,$y_5 = 45$,$y_6 = 30$,$y_7 = 15$,
故最多可摆$7$层。
第1层可摆$105\div10 = 10.5\approx10$(瓶);
第2层可摆$90\div10 = 9$(瓶);
第3层可摆$75\div10 = 7.5\approx7$(瓶);
第4层可摆$60\div10 = 6$(瓶);
第5层可摆$45\div10 = 4.5\approx4$(瓶);
第6层可摆$30\div10 = 3$(瓶);
第7层可摆$15\div10 = 1.5\approx1$(瓶)。
共$10 + 9+7 + 6+4 + 3+1 = 40$(瓶),
故该展台最多可摆$40$瓶葡萄酒。
15. 如图,已知$\triangle ABC$和$\triangle DEC$面积相等,点$E$在$BC$边上,$DE// AB$交$AC$于点$F$,$AB = 12$,$EF = 9$,则$DF$长为_______.

答案:
7【解析】$\because DE// AB$,$\therefore\triangle EFC\sim\triangle BAC$,
$\therefore\frac{S_{\triangle CEF}}{S_{\triangle ABC}}=(\frac{EF}{AB})^2=(\frac{9}{12})^2=\frac{9}{16}$。
$\because S_{\triangle ABC}=S_{\triangle DEC}$,$\therefore S_{\triangle EFC}=\frac{9}{16}S_{\triangle DEC}$,
$\therefore EF:ED = 9:16$。
$\because EF = 9$,$\therefore ED = 16$,$\therefore DF = 7$。
$\therefore\frac{S_{\triangle CEF}}{S_{\triangle ABC}}=(\frac{EF}{AB})^2=(\frac{9}{12})^2=\frac{9}{16}$。
$\because S_{\triangle ABC}=S_{\triangle DEC}$,$\therefore S_{\triangle EFC}=\frac{9}{16}S_{\triangle DEC}$,
$\therefore EF:ED = 9:16$。
$\because EF = 9$,$\therefore ED = 16$,$\therefore DF = 7$。
查看更多完整答案,请扫码查看


