《2025年北大绿卡九年级数学下册人教版》

11. 2023年新能源汽车继续保持快速增长，产销突破了900万辆，市场占有率超过30％，汽车出口再创新高，全年出口接近500万辆.为继续扩大销量，某城市新能源汽车销售商推出分期付款购车促销活动，交付首付款后，若余款在60个月内结清，则不计算利息.张先生在该销售商手上购买了一辆价值为20万元的新能源汽车，交了首付款后余款由平均每月付款$y$万元，$x$个月结清.$y$与$x$满足某函数关系，其部分对应值如下表，请回答下列问题.
|$x$/月|…|2|4|7|10|…|
|$y$/万元|…|7|3.5|2|1.4|…|
(1)确定$y$与$x$的函数解析式，并求出首付款.
(2)若张先生用40个月结清，则平均每月应付多少万元.
(3)如果张先生打算每月付款0.25万元，那么他能否在规定不计算利息的期限内结清余款?

答案： 【解】
(1)由表格猜想$y$与$x$成反比例函数关系，
设$y$与$x$的函数解析式为$y = \frac{k}{x}(k\neq0)$，
把$x = 2$，$y = 7$代入解析式，得$7 = \frac{k}{2}$，
∴$k = 14$，
∴$y$与$x$的函数解析式为$y = \frac{14}{x}(1\leq x\leq60$的整数)，
经检验表中其他各组对应值均满足此解析式，
∴当$x = 1$时，$y = 14$，
∴$20 - 14 = 6$(万元)，
∴首付款为 6 万元。
(2)当$x = 40$时，$y = \frac{14}{40} = 0.35$(万元)，
∴平均每月应付 0.35 万元。
(3)当$y = 0.25$时，$0.25 = \frac{14}{x}$，解得$x = 56$，
∵$56 ＜ 60$，
∴他能在规定不计算利息的期限内结清余款。

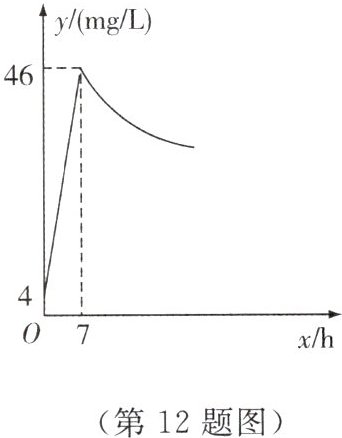
12. 近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO.在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4 mg/L，此后浓度呈直线型增加，在第7 h达到最高值46 mg/L时发生爆炸；爆炸后，空气中的CO浓度成反比例下降.如下图，根据题中相关信息回答下列问题.
(1)求爆炸前、后空气中CO浓度$y$与时间$x$的函数关系式，并写出相应自变量的取值范围.
(2)当空气中的CO浓度达到34 mg/L时，井下3 km的矿工接到自动报警信号，这时他们至少要以怎样的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时，才能回到矿井开展工作，求矿工至少在爆炸后多长时间才能下井.

答案： 【解】
(1)因为爆炸前$CO$浓度呈直线型增加，所以可设$y$与$x$的函数关系式为$y = k_{1}x + b(k_{1}\neq0)$。
由图象知$y = k_{1}x + b$的图象过点$(0,4)$与$(7,46)$，
则$\begin{cases}b = 4\\7k_{1}+b = 46\end{cases}$，解得$\begin{cases}k_{1} = 6\\b = 4\end{cases}$，
则$y = 6x + 4$，此时自变量$x$的取值范围是$0\leq x\leq7$($x = 7$可放在第二段函数中)。
∵爆炸后$CO$浓度成反比例下降，
∴可设$y$与$x$的函数关系式为$y = \frac{k_{2}}{x}(k_{2}\neq0)$。
由图象知$y = \frac{k_{2}}{x}$的图象过点$(7,46)$，
∴$\frac{k_{2}}{7} = 46$，
∴$k_{2} = 322$，
∴$y = \frac{322}{x}$，
此时自变量$x$的取值范围是$x ＞ 7$。
(2)当$y = 34$时，由$y = 6x + 4$，得$6x + 4 = 34$，解得$x = 5$。
∴撤离的最长时间为$7 - 5 = 2$(h)。
$3\div2 = 1.5(km/h)$。
故撤离的速度至少是$1.5\ km/h$。
(3)当$y = 4$时，由$y = \frac{322}{x}$，得$x = 80.5$，
$80.5 - 7 = 73.5$(h)。
∴矿工至少在爆炸后$73.5\ h$才能下井。

13. “人潮人海中，有你有我”，上下学的“停车大战”与“拥堵大戏”已成为社会热点问题.某校对本校下午放学校门口“堵塞”情况做了一次调查后发现：每天放学时间2分钟后校门外学生流量变化大致可以用“拥挤指数”$y(\%)$与放学后时间$x$(分)的函数关系描述.如图，2～12分钟函数图象为抛物线，且在第12分钟达到该函数最大值100，12分钟之后为函数$y=\frac{k}{x}(x ＞ 0)$的图象的一部分.
(1)求二次函数和反比例函数的解析式(需明确取值范围).
(2)若“拥挤指数”$y\geqslant36$，出于安全考虑，需要护学岗执勤人员维护秩序、疏导交通.请依据图象计算每天至少需要执勤的时间.

答案： 【解】
(1)由图象可知，二次函数图象的顶点坐标为$(12,100)$，
∴设二次函数解析式为$y = a(x - 12)^{2}+100$，
将点$(2,0)$代入二次函数的解析式，得$100a + 100 = 0$，
解得$a = - 1$，
∴二次函数解析式为$y = -(x - 12)^{2}+100(2\leq x ＜ 12)$。
将点$(12,100)$代入反比例函数解析式，得$100 = \frac{k}{12}$，解得$k = 1200$，
∴反比例函数的解析式为$y = \frac{1200}{x}(x\geq12)$。
(2)由$y = -(x - 12)^{2}+100 = 36$，
得$x = 4$或$x = 20$(舍)。
由$y = \frac{1200}{x} = 36$，得$x = \frac{100}{3}$。
∵$\frac{100}{3}-4 = \frac{88}{3}$，
∴每天至少需要执勤的时间为$\frac{88}{3}$分钟。