《2025年北大绿卡九年级数学下册人教版》

13. 如图，装有某种液体的工业用桶中放置有一根搅拌棍．工人师傅为了解桶内所装液体的体积，先在搅拌棍所处桶孔位置做好标记点$A$，并取出；然后测得搅拌棍接触到液体部分$BD = 1\ m$，搅拌棍$A$到底端$D$处的长度为$1.5\ m$，最后测量出桶的高$AE$为$1.2\ m$，圆桶内壁的底面直径为$1\ m$．已知桶内的液面与桶底面平行，其平面示意图如图2所示．请你根据以上数据，帮工人师傅计算出桶内所装液体的体积(结果保留$\pi$)．

答案： 【解】由题意，得$BC// DE$，
$\therefore\frac{BD}{AD}=\frac{CE}{AE}$，
$\therefore\frac{1}{1.5}=\frac{CE}{1.2}$，解得$CE = 0.8\ m$，
$\therefore$桶内所装液体的体积$=\pi(\frac{1}{2})^{2}\times0.8=\frac{1}{5}\pi(m^{3})$.
答：桶内所装液体的体积为$\frac{1}{5}\pi\ m^{3}$.

14. 如图，在$\triangle ABC$中，$AB = AC$，$AD\perp BC$于点$D$，$E$在$AD$上，$\frac{AE}{AD}=\frac{2}{5}$，$CE$的延长线交$AB$于点$F$，$DG// CF$．若$AB = 6\ cm$，求$GF$的长．

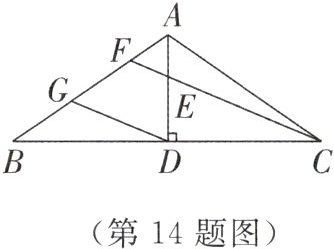
答案： 【解】$\because AB = AC$，$AD\perp BC$，$\therefore BD = DC$.
又$\because DG// CF$，
$\therefore\frac{BG}{GF}=\frac{BD}{DC}=1$，$\therefore BG = GF$.
$\because\frac{AE}{AD}=\frac{2}{5}$，$DG// CF$，$\therefore\frac{AF}{AG}=\frac{AE}{AD}=\frac{2}{5}$，
$\therefore AF=\frac{2}{3}GF$.
$\because AB = 6\ cm$，
$\therefore AF + GF + BG = 6$，即$\frac{2}{3}GF + GF + GF = 6$.
$\therefore GF=\frac{9}{4}\ cm$.

15. 如图，已知$AB = AD$，$AC = AE$，$FG// DE$．求证：$\triangle ABC\sim\triangle AFG$．

答案： 【证明】$\because AB = AD$，$\angle BAC=\angle DAE$，$AC = AE$，
$\therefore\triangle ABC\cong\triangle ADE$，$\therefore\angle B=\angle ADE$，
$\therefore DE// CB$.
$\because FG// DE$，$\therefore FG// CB$，$\therefore\triangle ABC\sim\triangle AFG$.