《2025年北大绿卡九年级数学下册人教版》

16. 如图，矩形$ABCD$的四个顶点都在格点(网格线的交点)上，对角线$AC$，$BD$相交于点$E$，反比例函数$y = \frac{k}{x}(x ＞ 0)$的图象经过点$A$。

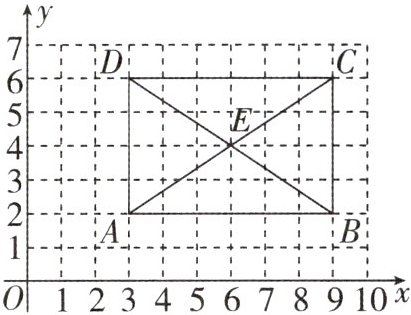
(第16题图)
(1)求这个反比例函数的解析式。
(2)请先描出这个反比例函数图象上不同于点$A$的三个格点，再画出反比例函数的图象。
(3)将矩形$ABCD$向左平移，当点$E$落在这个反比例函数的图象上时，平移的距离为_______。

答案：
【解】
(1)
∵反比例函数$y = \frac{k}{x}$的图象经过点$A(3,2)$，
∴$2 = \frac{k}{3}$，
∴$k = 6$，
∴这个反比例函数的解析式为$y = \frac{6}{x}$.
(2)当$x = 1$时，$y = 6$，
当$x = 2$时，$y = 3$，
当$x = 6$时，$y = 1$，
∴反比例函数$y = \frac{6}{x}$的图象经过$(1,6)$，$(2,3)$，$(6,1)$.
画图如下：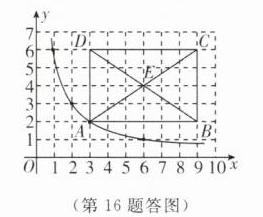
(3)
∵$E(6,4)$向左平移后，$E$在反比例函数的图象上，
∴平移后点$E$对应点的纵坐标为$4$，
当$y = 4$时，$4 = \frac{6}{x}$，解得$x = \frac{3}{2}$，
∴平移距离为$6 - \frac{3}{2} = \frac{9}{2}$.
故答案为$\frac{9}{2}$.