《2025年北大绿卡九年级数学下册人教版》

5.某地上年度电价为0.8元/度,年用电量为1亿度﹐本年度计划将电价调至0.55~0.75元/度之间,经测算,若电价调至工元/度,则本年度新增的电量为y(亿度)与(式—0.4)(元/度)成反比例关系﹐且当r=0.65时,y=0.8.(1)求y与:之间的函数关系式;(2)若每度电的成本价为0.3元,电价调至0.6元/度,请你预算本年度电力部门的纯收入.[纯收人=用电量×(实际电价―成本价)]

答案： 【解】
(1)由题意设$y = \frac{k}{x - 0.4}$. 当$x = 0.65$时，$y = 0.8$， 则$0.8 = \frac{k}{0.65 - 0.4}$，解得$k = 0.2$，故$y$与$x$之间的函数关系式为$y = \frac{0.2}{x - 0.4}$.
(2)由题意可得$x = 0.6$，则$y = \frac{0.2}{0.6 - 0.4} = 1$，故总用电量为$2$亿度，故本年度电力部门的纯收入为$2\times(0.6 - 0.3)=0.6$(亿元). 

6. 家用电灭蚊器的发热部分使用了PTC发热材料，它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示. 通电后，发热材料的温度在由室温10 ℃上升到30 ℃的过程中，电阻与温度成反比例关系，且在温度达到30 ℃时，电阻下降到最小值；随后电阻随温度升高而增加，温度每上升1 ℃，电阻增加$\frac{4}{15}$ kΩ.
(1)求当10≤t≤30时，R和t之间的函数关系式；
(2)求温度在30 ℃时电阻R的值，并求出t≥30时，R和t之间的关系式；
(3)家用电灭蚊器在使用过程中，温度在什么范围内时，发热材料的电阻不超过6 kΩ?
[img id=第6题图]

答案： 【解】
(1)$\because$温度在由室温$10^{\circ}\text{C}$上升到$30^{\circ}\text{C}$的过程中，电阻与温度成反比例关系，
$\therefore$可设$R$和$t$之间的关系式为$R = \frac{k}{t}$，将$(10,6)$代入上式，得$6 = \frac{k}{10}$，解得$k = 60$.
故当$10\leq t\leq30$时，$R = \frac{60}{t}$.
(2)当$t = 30$时，$R = \frac{60}{30} = 2$，
$\therefore$温度在$30^{\circ}\text{C}$时，电阻$R$为$2\text{ k}\Omega$.
$\because$温度达到$30^{\circ}\text{C}$时，电阻下降到最小值，随后电阻随温度升高而增加，温度每上升$1^{\circ}\text{C}$，电阻增加$\frac{4}{15}\text{ k}\Omega$，
$\therefore$当$t\geq30$时，$R = 2+\frac{4}{15}(t - 30)=\frac{4}{15}t - 6$.
(3)把$R = 6$代入$R = \frac{4}{15}t - 6$，得$t = 45$，
$\therefore$温度在$10^{\circ}\text{C}～45^{\circ}\text{C}$(包括两端值)时，电阻不超过$6\text{ k}\Omega$.

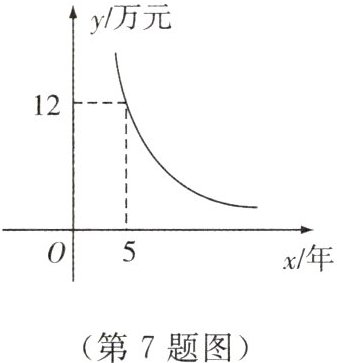
7. 小明家利用国家贷款100万元，购买了某山庄的一套住房，在付了首期款后，每年需向银行付款y万元，预计x年后结清余款，y与x的函数关系如图所示，试根据图象所提供的信息，回答下列问题.
(1)确定y与x之间的函数解析式，并说明小明家付了多少万元首期款.
(2)小明家若计划用15年时间结清余款，那么每年应向银行付多少万元?
(3)若打算每年付款不超过6万元，小明家至少要多少年才能结清余款?
[img id=第7题图]

答案： 【解】
(1)设$y = \frac{k}{x}$，把点$(5,12)$代入，得$k = 60$，
所以$y = \frac{60}{x}$.
因为$100 - 60 = 40$，所以小明家付了$40$万元首期款.
(2)当$x = 15$时，$y = 4$，那么每年应向银行付$4$万元.
(3)当$y\leq6$时，$x\geq10$，即小明家至少要$10$年才能结清余款.