《2025年北大绿卡九年级数学下册人教版》

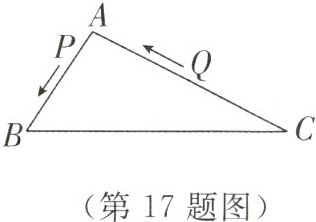
17. 如图，△ABC中，AB = 8厘米，AC = 16厘米，点P从A点出发，以每秒2厘米的速度向B点运动，点Q从C点同时出发，以每秒3厘米的速度向A点运动，其中一个动点到端点时，另一个动点也相应停止运动，设运动的时间为t. (1)用含t的代数式表示：AP=________，AQ=________. (2)当以A，P，Q为顶点的三角形与△ABC相似时，求运动时间是多少？

答案： 【解】
(1)$AP = 2t,AQ = 16 - 3t$.
(2)$\because\angle PAQ=\angle BAC$,
$\therefore$当$\frac{AP}{AB}=\frac{AQ}{AC}$时,$\triangle APQ\sim\triangle ABC$,
即$\frac{2t}{8}=\frac{16 - 3t}{16}$,解得$t=\frac{16}{7}$秒.
当$\frac{AP}{AC}=\frac{AQ}{AB}$时,$\triangle APQ\sim\triangle ACB$,
即$\frac{2t}{16}=\frac{16 - 3t}{8}$,解得$t = 4$秒.
$\therefore$运动时间为$\frac{16}{7}$秒或4秒.

18. 如图，在平面直角坐标系中，已知OA = 12 cm，OB = 6 cm，点P从O点开始沿OA边向点A以1 cm/s的速度移动，点Q从点B开始沿BO边向点O以1 cm/s的速度移动，如果P，Q同时出发，用t(单位：s)表示移动的时间(0≤t≤6)，那么：(1)当t为何值时，△POQ与△AOB相似. (2)设△POQ的面积为y，求y与t的函数解析式，并求△POQ面积的最大值.

答案： 【解】
(1)$\because OB = 6\ cm,BQ = t\ cm$,
$\therefore OQ=OB - BQ=(6 - t)\ cm$.
$\because OP = t\ cm$,
当$\triangle POQ\sim\triangle AOB$时,$\frac{OQ}{OB}=\frac{OP}{OA}$,即$\frac{6 - t}{6}=\frac{t}{12}$,
解得$t = 4$,
$\therefore$当$t = 4$时,$\triangle POQ$与$\triangle AOB$相似.
当$\triangle POQ\sim\triangle BOA$时,$\frac{OQ}{OA}=\frac{OP}{OB}$,
即$\frac{6 - t}{12}=\frac{t}{6}$,解得$t = 2$,
$\therefore$当$t = 2$时,$\triangle POQ$与$\triangle BOA$相似.
综上所述,当$t = 4\ s$或$t = 2\ s$时,$\triangle POQ$与$\triangle AOB$相似.
(2)$S_{\triangle POQ}=\frac{1}{2}OP\times OQ=\frac{1}{2}t\times(6 - t)=-\frac{1}{2}t^{2}+3t$,
$\therefore y=-\frac{1}{2}t^{2}+3t(0\leqslant t\leqslant6)$,
$\therefore y=-\frac{1}{2}(t - 3)^{2}+\frac{9}{2}(0\leqslant t\leqslant6)$,
$\therefore$当$t = 3$时,$y$取得最大值,
$\therefore\triangle POQ$面积的最大值是$\frac{9}{2}$.