第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
20. 已知BD为等腰三角形ABC的腰AC上的高,BD = 1,tan∠ABD = \sqrt{3},求CD的长.
答案:
【解】分三种情况:
①如答图 1,当$\angle BAC$为钝角,$AB = AC$时,
在$Rt\triangle ABD$中,$\because BD = 1$,$\tan\angle ABD = \sqrt{3}$,
$\therefore AD = \sqrt{3}$,$\therefore AB = 2$,$\therefore AC = 2$,$\therefore CD = 2 + \sqrt{3}$.
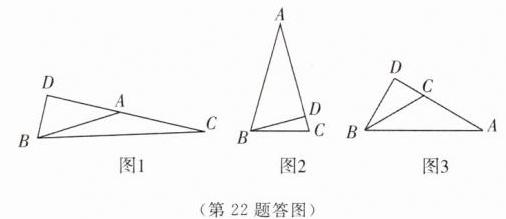
②如答图 2,当$\angle A$为锐角,$AB = AC$时,
在$Rt\triangle ABD$中,$\because BD = 1$,$\tan\angle ABD = \sqrt{3}$,
$\therefore AD = \sqrt{3}$,$\therefore AB = 2$,$\therefore AC = 2$,$\therefore CD = 2 - \sqrt{3}$.
③如答图 3,当$\angle A$为底角,$BC = AC$时,
$\because\tan\angle ABD = \sqrt{3}$,
$\therefore\angle ABD = 60^{\circ}$.$\because BD\perp AD$,$\therefore\angle A = 30^{\circ}$.
$\because BC = AC$,$\therefore\angle ABC = \angle A = 30^{\circ}$.
$\therefore\angle BCD = \angle A + \angle ABC = 60^{\circ}$.$\because BD = 1$,$\therefore CD = \frac{\sqrt{3}}{3}$.
综上所述,$CD$的长为$2 + \sqrt{3}$或$2 - \sqrt{3}$或$\frac{\sqrt{3}}{3}$.
【解】分三种情况:
①如答图 1,当$\angle BAC$为钝角,$AB = AC$时,
在$Rt\triangle ABD$中,$\because BD = 1$,$\tan\angle ABD = \sqrt{3}$,
$\therefore AD = \sqrt{3}$,$\therefore AB = 2$,$\therefore AC = 2$,$\therefore CD = 2 + \sqrt{3}$.

②如答图 2,当$\angle A$为锐角,$AB = AC$时,
在$Rt\triangle ABD$中,$\because BD = 1$,$\tan\angle ABD = \sqrt{3}$,
$\therefore AD = \sqrt{3}$,$\therefore AB = 2$,$\therefore AC = 2$,$\therefore CD = 2 - \sqrt{3}$.
③如答图 3,当$\angle A$为底角,$BC = AC$时,
$\because\tan\angle ABD = \sqrt{3}$,
$\therefore\angle ABD = 60^{\circ}$.$\because BD\perp AD$,$\therefore\angle A = 30^{\circ}$.
$\because BC = AC$,$\therefore\angle ABC = \angle A = 30^{\circ}$.
$\therefore\angle BCD = \angle A + \angle ABC = 60^{\circ}$.$\because BD = 1$,$\therefore CD = \frac{\sqrt{3}}{3}$.
综上所述,$CD$的长为$2 + \sqrt{3}$或$2 - \sqrt{3}$或$\frac{\sqrt{3}}{3}$.
21. 阅读下列材料:
在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,求证:\frac{a}{\sin A} = \frac{b}{\sin B}.
证明:如图1,过点C作CD⊥AB于点D,则:
在Rt△BCD中,CD = asin B,
在Rt△ACD中,CD = bsin A,
∴asin B = bsin A,
∴\frac{a}{\sin A} = \frac{b}{\sin B}.
根据上面的材料解决下列问题:
(1)如图2,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,求证:\frac{b}{\sin B} = \frac{c}{\sin C};
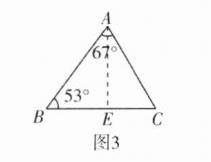
(2)为了办好湖南省首届旅游发展大会,张家界市积极优化旅游环境. 如图3,规划中的一片三角形区域需美化,已知∠A = 67°,∠B = 53°,AC = 80 m,求这片区域的面积.(结果保留根号. 参考数据:sin 53°≈0.8,sin 67°≈0.9)

在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,求证:\frac{a}{\sin A} = \frac{b}{\sin B}.
证明:如图1,过点C作CD⊥AB于点D,则:
在Rt△BCD中,CD = asin B,
在Rt△ACD中,CD = bsin A,
∴asin B = bsin A,
∴\frac{a}{\sin A} = \frac{b}{\sin B}.
根据上面的材料解决下列问题:
(1)如图2,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,求证:\frac{b}{\sin B} = \frac{c}{\sin C};
(2)为了办好湖南省首届旅游发展大会,张家界市积极优化旅游环境. 如图3,规划中的一片三角形区域需美化,已知∠A = 67°,∠B = 53°,AC = 80 m,求这片区域的面积.(结果保留根号. 参考数据:sin 53°≈0.8,sin 67°≈0.9)

答案:
(1)【证明】如答图 1,过点$A$作$AD\perp BC$于点$D$,则:
在$Rt\triangle ABD$中,$AD = c\sin B$,
在$Rt\triangle ACD$中,$AD = b\sin C$,
$\therefore c\sin B = b\sin C$,$\therefore\frac{b}{\sin B} = \frac{c}{\sin C}$.

(第 21 题答图 1)
(2)【解】如答图 2,过点$A$作$AE\perp BC$于点$E$.
$\because\angle BAC = 67^{\circ}$,$\angle B = 53^{\circ}$,
$\therefore\angle C = 60^{\circ}$.
在$Rt\triangle ACE$中,$AE = AC\cdot\sin 60^{\circ} = 80\times\frac{\sqrt{3}}{2} = 40\sqrt{3}(m)$.
又$\because\frac{AC}{\sin B} = \frac{BC}{\sin\angle BAC}$,即$\frac{80}{0.8} = \frac{BC}{0.9}$,
$\therefore BC = 90\ m$,
$\therefore S_{\triangle ABC} = \frac{1}{2}\times90\times40\sqrt{3} = 1800\sqrt{3}(m^{2})$.
(第 21 题答图 2)
答:这片区域的面积是$1800\sqrt{3}\ m^{2}$.
(1)【证明】如答图 1,过点$A$作$AD\perp BC$于点$D$,则:
在$Rt\triangle ABD$中,$AD = c\sin B$,
在$Rt\triangle ACD$中,$AD = b\sin C$,
$\therefore c\sin B = b\sin C$,$\therefore\frac{b}{\sin B} = \frac{c}{\sin C}$.

(第 21 题答图 1)
(2)【解】如答图 2,过点$A$作$AE\perp BC$于点$E$.
$\because\angle BAC = 67^{\circ}$,$\angle B = 53^{\circ}$,
$\therefore\angle C = 60^{\circ}$.
在$Rt\triangle ACE$中,$AE = AC\cdot\sin 60^{\circ} = 80\times\frac{\sqrt{3}}{2} = 40\sqrt{3}(m)$.
又$\because\frac{AC}{\sin B} = \frac{BC}{\sin\angle BAC}$,即$\frac{80}{0.8} = \frac{BC}{0.9}$,
$\therefore BC = 90\ m$,
$\therefore S_{\triangle ABC} = \frac{1}{2}\times90\times40\sqrt{3} = 1800\sqrt{3}(m^{2})$.

(第 21 题答图 2)
答:这片区域的面积是$1800\sqrt{3}\ m^{2}$.
查看更多完整答案,请扫码查看


