《2025年北大绿卡九年级数学下册人教版》

1. 在Rt△ABC中，∠C = 90°，AB = 5，BC = 3，则cos B的值是（ ）.
A. $\frac{3}{5}$
B. $\frac{4}{5}$
C. $\frac{3}{4}$
D. $\frac{4}{3}$

答案： A

2. 在△ABC中，∠C = 90°，tan A = 2，则cos A的值为（ ）.
A. $\frac{\sqrt{5}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{1}{2}$

答案： A

3. 2024年5月29日16时12分，“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射. 当火箭上升到点A时，位于海平面R处的雷达测得点R到点A的距离为a千米，仰角为θ，则此时火箭距海平面的高度AL为（ ）.

A. $a\sin\theta$千米
B. $\frac{a}{\sin\theta}$千米
C. $a\cos\theta$千米
D. $\frac{a}{\cos\theta}$千米

答案： A

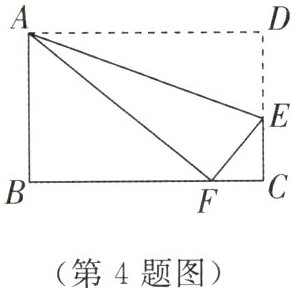
4. 如图，在矩形ABCD中，AB = 6，BC = 8，点E在DC上，把△ADE沿AE折叠，点D恰好落在BC边上的点F处，则cos∠CEF的值为（ ）.

A. $\frac{\sqrt{7}}{4}$
B. $\frac{\sqrt{7}}{3}$
C. $\frac{3}{4}$
D. $\frac{5}{4}$

答案： A 【解析】
∵ 四边形 ABCD 是矩形，
∴AD = BC = 8，DC = AB = 6.
∵ 把△ADE 沿 AE 折叠，点 D 恰好落在 BC 边上的点 F 处，
∴AF = AD = 8，EF = DE，
∴BF = $\sqrt{AF^{2}-AB^{2}}=\sqrt{8^{2}-6^{2}} = 2\sqrt{7}$，
∴CF = BC - BF = 8 - 2\sqrt{7}.
在 Rt△EFC 中，CE = DC - DE = 6 - EF，
由勾股定理，得 EF² = CE² + CF²，
∴EF² = (6 - EF)² + (8 - 2\sqrt{7})²，
∴EF = $\frac{32 - 8\sqrt{7}}{3}$，
∴CE = 6 - $\frac{32 - 8\sqrt{7}}{3}=\frac{8\sqrt{7}-14}{3}$，
∴cos∠CEF = $\frac{CE}{EF}=\frac{\frac{8\sqrt{7}-14}{3}}{\frac{32 - 8\sqrt{7}}{3}}=\frac{\sqrt{7}}{4}$.
故选 A.

5. 如图所示，在Rt△ABC中，∠C = 90°，AB = 6，BC = 4，求cos A，cos B的值.

答案： 【解】
∵∠C = 90°，AB = 6，BC = 4，
∴cos B = $\frac{2}{3}$，AC = 2\sqrt{5}，
∴cos A = $\frac{\sqrt{5}}{3}$.

6. 在Rt△ABC中，∠C = 90°，AB = 5，BC = 3，那么tan A的值是（ ）.
A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$

答案： A

7. 如图是一把圆规的平面示意图，OA是支撑臂，OB是旋转臂. 已知OA = OB = 10，使用时，以点A为支撑点，笔芯端点B可绕点A旋转作出圆. 若支撑臂与旋转臂的夹角∠AOB = 2θ，则圆规能画出的圆的半径AB的长度为（ ）.

A. 20tanθ
B. 10tan 2θ
C. 20sinθ
D. 10sin 2θ

答案： C